狭义相对论中的速度变换
fengxiaot Lv4
  2021-01-20 12:09:08 2021-01-20 12:09  

这篇文章本来是高二时候写的，当初对狭义相对论理解不深，所以把《奥赛物理题选》上的一道简单题在各种参考系下算了一遍以理清思路熟悉变换。现在拿来练练Markdown语法吧！

题目

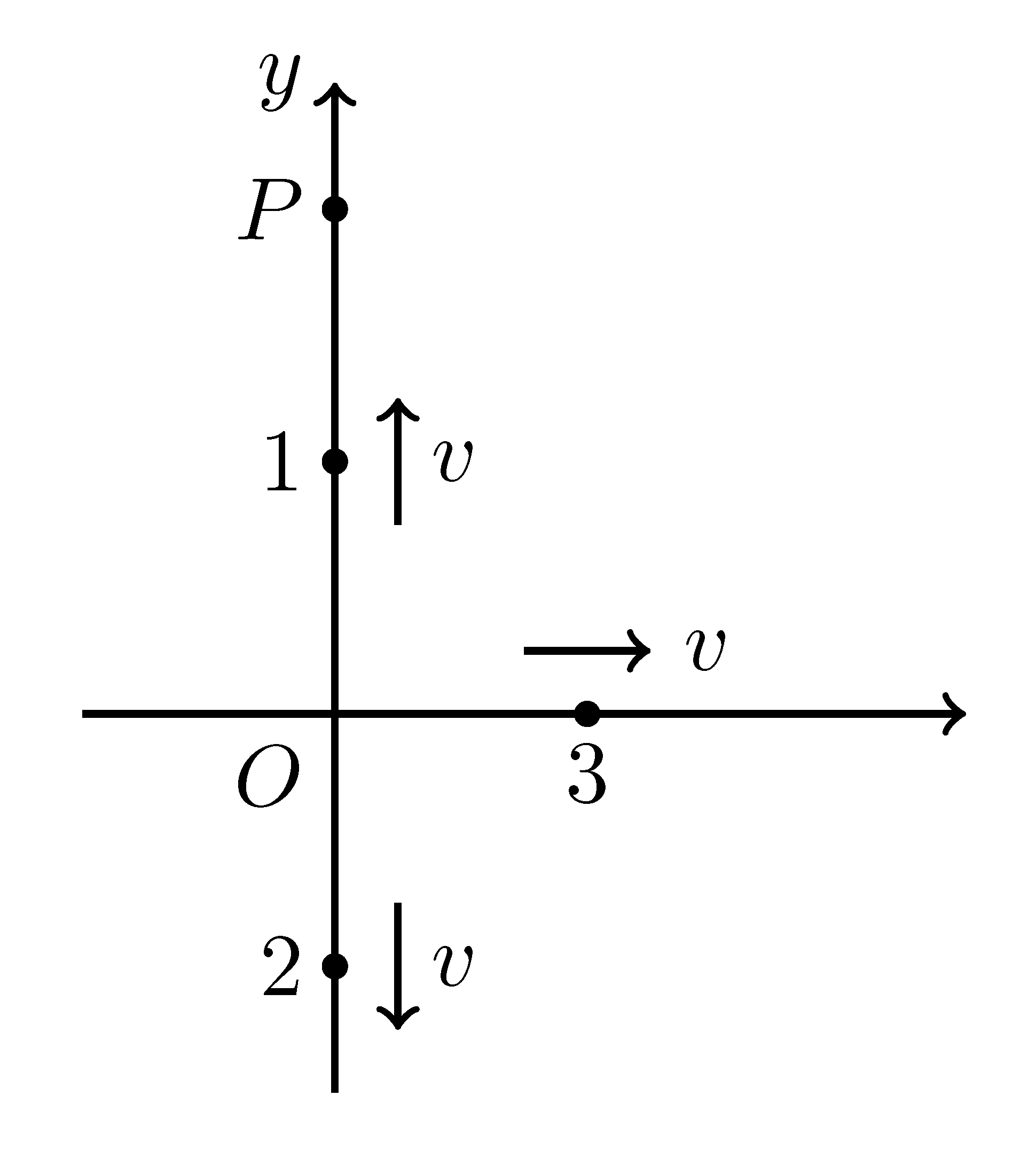
惯性系 SS 中三艘已处于匀速直线运动状态的飞船 1,2,31,2,3，各自的速度大小同为 vv，航向已在图中标出。某时刻三艘飞船“相聚”（彼此靠近，但不相碰）与 SS 系的 OO 点。此时各自时钟都校准在零点。飞船 11 到达图中与 OO 点相距 ll 的 PP 处时，发出两束无线电信号。而后分别被飞船 2,32,3 接受到。
(1) 在飞船 11 中确定发射信号的时刻 t1t_1；
(2) 在飞船 22 中确定接收信号的时刻 t2t_2；
(3) 在飞船 33 中确定接收信号的时刻 t3t_3。


第一小问

SS 系中飞船 11 从 OO 点到达 PP 点所经过的时间为

t1S=lvt_{1S} = \frac{l}{v}

在飞船 11 中确定发射信号的时刻，则飞船 11 参考系从出发到发射信号，经历的时间是本征的

t1S=t11−β2t_{1S} = \dfrac{t_1}{\sqrt{1-\beta^2}}

所以有

t1=lv1−β2t_1 = \dfrac{l}{v} \sqrt{1-\beta^2}


第二小问

法一：在惯性系中讨论

由简单的追及问题知识，在 SS 系中飞船 22 收到信号的时间为

t2S=lv+2lc−vt_{2S} = \frac{l}{v} + \frac{2l}{c-v}

飞船 22 参考系中飞船 22 始终不动，即 Δx2′=0\Delta x_2'=0 ，故 t2t_2 本征

Δt2S=Δt2+vc2Δx2′1−β2\Delta t_{2S} = \frac{\Delta t_2 + \frac{v}{c^2} \Delta x_2' }{\sqrt{1-\beta^2}}

所以由钟慢效应

t2=t2S1−β2=(lv+2lc−v)1−β2=lvc+vc−v1−β2t_2 = t_{2S} \sqrt{1-\beta^2} = \left( \frac{l}{v} + \frac{2l}{c-v} \right) \sqrt{1-\beta^2} = \frac{l}{v} \frac{c+v}{c-v} \sqrt{1-\beta^2}

法二：在飞船 2 参考系中讨论

飞船 11 相对于飞船 22 的速度为

v12=2v1+v2c2=2vc2c2+v2v_{12}=\frac{2 v}{1+\frac{v^{2}}{c^{2}}}=\frac{2 v c^{2}}{c^{2}+v^{2}}

在飞船 22 参考系中，飞船 11 到达 PP 点用了

Δt1=t11−v122/c2=lv1−β21−4v2c2(c2+v2)2=lv1−β2c2+v2c2−v2\Delta t_{1}=\frac{t_{1}}{\sqrt{1-v_{12}^{2} / c^{2}}}=\frac{\frac{l}{v} \sqrt{1-\beta^{2}}}{\sqrt{1-\frac{4 v^{2} c^{2}}{\left(c^{2}+v^{2}\right)^{2}}}}=\frac{l}{v} \sqrt{1-\beta^{2}} \frac{c^{2}+v^{2}}{c^{2}-v^{2}}

其中在 22 系中，飞船 22 认为飞船 11 走了 v12Δt1v_{12} \Delta t_1 才发射信号。光速始终为 cc，所以从飞船 11 发射到飞船 22 接收信号用了时间

Δt2=v12Δt1c=2vc2c2+v2lvc2+v2c2−v21−β21c=lv1−β22vcc2−v2\Delta t_{2}=\frac{v_{12} \Delta t_{1}}{c}=\frac{2 v c^{2}}{c^{2}+v^{2}} \frac{l}{v} \frac{c^{2}+v^{2}}{c^{2}-v^{2}} \sqrt{1-\beta^{2}} \frac{1}{c}=\frac{l}{v} \sqrt{1-\beta^{2}} \frac{2 v c}{c^{2}-v^{2}}

t2=Δt1+Δt2=lv1−β2(c2+v2c2−v2+2vcc2−v2)=lvc+vc−v1−β2t_{2}=\Delta t_{1}+\Delta t_{2}=\frac{l}{v} \sqrt{1-\beta^{2}}\left(\frac{c^{2}+v^{2}}{c^{2}-v^{2}}+\frac{2 v c}{c^{2}-v^{2}}\right)=\frac{l}{v} \frac{c+v}{c-v} \sqrt{1-\beta^{2}}

法三：在飞船 1 参考系中讨论

飞船 22 相对于飞船 11 的速度为

v21=v12=2v1+v2c2=2vc2c2+v2v_{21}=v_{12}=\frac{2 v}{1+\frac{v^{2}}{c^{2}}}=\frac{2 v c^{2}}{c^{2}+v^{2}}

当飞船 11 发出信号时，在 11 系中，时间过了

Δt1=t1=lv1−β2\Delta t_1 = t_1 = \dfrac{l}{v} \sqrt{1-\beta^2}

此时飞船 22 行进了 v21Δt1v_{21}\Delta t_1，则从 11 发出信号到 22 接收信号，时间过了

Δt2=v21Δt1c−v21\Delta t_{2}=\frac{v_{21} \Delta t_{1}}{c-v_{21}}

这是简单的追及问题。从一切开始到飞船 22 接收信号，在 11 系中一共过了

Δt=v21Δt1c−v21+Δt1=cΔt1c−v21=c2+v2(c−v)2lv1−β2\Delta t=\frac{v_{21} \Delta t_{1}}{c-v_{21}}+\Delta t_{1}=\frac{c \Delta t_{1}}{c-v_{21}}=\frac{c^{2}+v^{2}}{(c-v)^{2}} \frac{l}{v} \sqrt{1-\beta^{2}}

变换回 22 系，t2t_2 为本征时间

t2=Δt1−v122/c2=c2+v2(c−v)2lv1−β2c2−v2c2+v2=lvc+vc−v1−β2t_{2}=\Delta t \sqrt{1-v_{12}^{2} / c^{2}}=\frac{c^{2}+v^{2}}{(c-v)^{2}} \frac{l}{v} \sqrt{1-\beta^{2}} \frac{c^{2}-v^{2}}{c^{2}+v^{2}}=\frac{l}{v} \frac{c+v}{c-v} \sqrt{1-\beta^{2}}


第三小问

法一：在惯性系中讨论

设从飞船 11 发射信号始，至飞船 33 收到信号止，于 SS 系中经过了时间 τ\tau 。
在三角形中，由余弦定理得

(2l)2+(vτ)2−22lvτcos⁡135∘=(cτ)2(\sqrt{2} l)^{2}+(v \tau)^{2}-2 \sqrt{2} l v \tau \cos 135^{\circ}=(c \tau)^{2}

(c2−v2)τ2−2vlτ−2l2=0\left(c^{2}-v^{2}\right) \tau^{2}-2 v l \tau-2 l^{2}=0

利用二次方程求根公式，代入舍去负根得

τ=vl+l2c2−v2c2−v2\tau=\frac{v l+l \sqrt{2 c^{2}-v^{2}}}{c^{2}-v^{2}}

所以总时间为

t3S=τ+t1S=vl+l2c2−v2c2−v2+lvt_{3 S}=\tau+t_{1 S}=\frac{v l+l \sqrt{2 c^{2}-v^{2}}}{c^{2}-v^{2}}+\frac{l}{v}

变换到 33 系，t3t_3 为本征时间

t3=t3S1−β2=l1−β2(v+2c2−v2c2−v2+1v)=lc1−β2(1β+β+2−β21−β2)t_{3}=t_{3 S} \sqrt{1-\beta^{2}}=l \sqrt{1-\beta^{2}}\left(\frac{v+\sqrt{2 c^{2}-v^{2}}}{c^{2}-v^{2}}+\frac{1}{v}\right)=\frac{l}{c} \sqrt{1-\beta^{2}}\left(\frac{1}{\beta}+\frac{\beta+\sqrt{2-\beta^{2}}}{1-\beta^{2}}\right)

法二：以飞船 3 为参考系

由相对论速度变换，可得

v13x=v+01+v⋅0c2=v,v13y=v1−β21+0=v1−β2v_{13 x}=\frac{v+0}{1+v \cdot \frac{0}{c^{2}}}=v, v_{13 y}=\frac{v \sqrt{1-\beta^{2}}}{1+0}=v \sqrt{1-\beta^{2}}

所以 11 系相对 33 系的速度为

v13=v13x2+v13y2=v2−β2v_{13}=\sqrt{v_{13x}^2+v_{13y}^2}=v\sqrt{2-\beta^2}

变换 xx 轴方向至与 v13⃗\vec{v_{13}} 方向相同，余下的分析过程与第二小问法二类似

Δt1=t11−v132/c2=lv1−β2(1−β2)2=lv1−β2\Delta t_{1}=\frac{t_{1}}{\sqrt{1-v_{13}^{2} / c^{2}}}=\frac{\frac{l}{v} \sqrt{1-\beta^{2}}}{\sqrt{\left(1-\beta^{2}\right)^{2}}}=\frac{l}{v \sqrt{1-\beta^{2}}}

Δt2=Δt1v13c=l2−β2c1−β2\Delta t_{2}=\frac{\Delta t_{1} v_{13}}{c}=\frac{l \sqrt{2-\beta^{2}}}{c \sqrt{1-\beta^{2}}}

所以总时间为

t3=Δt1+Δt2=lv1−β2+l2−β2c1−β2=lc1−β2(1β+β+2−β21−β2)t_{3}=\Delta t_{1}+\Delta t_{2}=\frac{l}{v \sqrt{1-\beta^{2}}}+\frac{l \sqrt{2-\beta^{2}}}{c \sqrt{1-\beta^{2}}}=\frac{l}{c} \sqrt{1-\beta^{2}}\left(\frac{1}{\beta}+\frac{\beta+\sqrt{2-\beta^{2}}}{1-\beta^{2}}\right)

法三：以飞船 1 为参考系

v31=v13=v2−β2v_{31}=v_{13}=v\sqrt{2-\beta^2}

变换 xx 轴方向至与 v31⃗\vec{v_{31}} 方向相同，余下的分析过程与第二小问法三类似

Δt1=t1=lv1−β2\Delta t_{1}=t_{1}=\frac{l}{v} \sqrt{1-\beta^{2}}

Δt=v31Δt1c−v31+Δt1=cΔt1c−v31=cc−v2−β2lv1−β2\Delta t=\frac{v_{31} \Delta t_{1}}{c-v_{31}}+\Delta t_{1}=\frac{c \Delta t_{1}}{c-v_{31}}=\frac{c}{c-v \sqrt{2-\beta^{2}}} \frac{l}{v} \sqrt{1-\beta^{2}}

变换到 33 系，t3t_3 为本征时间

t3=Δt1−v312/c2=cc−v2−β2lv1−β2(1−β2)=lc1−β2(1β+β+2−β21−β2)t_{3}=\Delta t \sqrt{1-v_{31}^{2} / c^{2}}=\frac{c}{c-v \sqrt{2-\beta^{2}}} \frac{l}{v} \sqrt{1-\beta^{2}}\left(1-\beta^{2}\right)=\frac{l}{c} \sqrt{1-\beta^{2}}\left(\frac{1}{\beta}+\frac{\beta+\sqrt{2-\beta^{2}}}{1-\beta^{2}}\right)


小结

  1. 飞船 11 从出发到发射信号经过的时间在 SS 系，11 系，22 系，33 系中各不相同，分别为

lv,lv1−β2,lv1−β2c2+v2c2−v2,lv1−β2\frac{l}{v}, \frac{l}{v}\sqrt{1-\beta^2}, \frac{l}{v}\sqrt{1-\beta^2}\frac{c^2+v^2}{c^2-v^2}, \frac{l}{v\sqrt{1-\beta^2}}

  1. 钟慢效应公式的应用一定要建立在某一个对象在某一个参考系中静止