线性代数讲义（二）分块矩阵与秩不等式

2021年暑假，受仲英书院学辅邀请，我主持了三次线性代数沙龙，对象是工科专业的本科一年级学生。这是第二次沙龙的讲义，主题是分块矩阵与秩不等式。分块是线性代数中重要的矩阵证明技巧，秩不等式则可用来估计零空间或解空间维数。恰逢线性代数期中考试，这二者都在应试中十分常用，希望能够给学弟学妹带来一些帮助。

分块矩阵概述

分块矩阵的定义

分块矩阵是线性代数中的一个重要内容，是处理矩阵的重要工具。

把一个矩阵 $A$ 的行分成若干组，列也分成若干组，从而 $A$ 被分成若干个子矩阵，把 $A$ 看成是由这些子矩阵组成的，这称为矩阵的分块。这种由子矩阵组成的矩阵叫做分块矩阵。

分块矩阵的运算

转置

分块矩阵应当先转置矩阵的子块，再对每个子块内部的元素进行转置，即

$$A = \begin{bmatrix} A_{11} & A_{12} & \cdots & A_{1n} \\ A_{21} & A_{22} & \cdots & A_{2n} \\ \vdots & \vdots & & \vdots\\ A_{m1} & A_{m2} & \cdots & A_{mn} \end{bmatrix} \Longrightarrow A^{T} = \begin{bmatrix} A_{11}^T & A_{21}^T & \cdots & A_{m1}^T \\ A_{12}^T & A_{22}^T & \cdots & A_{m2}^T \\ \vdots & \vdots & & \vdots\\ A_{1n}^T & A_{2n}^T & \cdots & A_{mn}^T \end{bmatrix}$$

乘法

将对应的子块按照矩阵乘法法则相乘即可，但需满足

• 左矩阵的列组数等于右矩阵的行组数
• 左矩阵的每个列组所含列数等于右矩阵的相应行组所含行数

分块对角矩阵

为什么

分块对角矩阵是除对角矩阵外形式最简单的矩阵，易于研究。

• 对于不可对角化的矩阵，我们总是希望把矩阵化成分块对角矩阵，比如Jordan标准形，有理标准形。
• 若能将线性空间 $V$ 分解为线性变换 $\mathcal{A}$ 的一系列不变子空间的直和，那么在这些不变子空间中各取一个基组成全空间 $V$ 的一个基，那么线性变换 $\mathcal{A}$ 在这组基下的矩阵就会是分块对角矩阵。
• 作为物理系的学生，在量子力学中分块对角矩阵也很常见，如果两个观察算符 $A$ 和 $B$ 是可对易的，那么把 $A$ 算符的各本征值的本征矢排列在一起，便能够形成态空间的一个基，且算符 $B$ 在这组基下的矩阵也是分块对角矩阵。

定义

设 $A$ 为 $n$ 阶矩阵，若 $A$ 的分块矩阵只有在主对角线上有非零子块，其余子块都为零矩阵，且非零子块都是方阵，即

$$A = \begin{bmatrix} A_1 & & & \\ & A_2 & & \\ & & \ddots & \\ & & & A_s \end{bmatrix} = \operatorname{diag} \left\{A_1,A_2,\cdots,A_s\right\}$$

其中 $A_i$ 是方阵，空白处都是零矩阵，则称 $A$ 为分块对角矩阵。

性质

1. $\det(A) = \det(A_1) \det(A_2) \cdots \det(A_s)$
2. $A^{-1} = \begin{bmatrix} A_1^{-1} & & & \\ & A_2^{-1} & & \\ & & \ddots & \\ & & & A_s^{-1} \end{bmatrix}$

分块初等矩阵

与初等变换对应着初等矩阵类似，分块初等变换也对应着分块初等矩阵。

分块矩阵的初等行变换包括：

1. 把一个块行的左 $P$ 倍加到另一个块行上，例如

   $$\begin{bmatrix} A_1 & A_2 \\ A_3 & A_4 \end{bmatrix} \xrightarrow{P\cdot (1)+(2)} \begin{bmatrix} A_1 & A_2 \\ PA_1 + A_3 & PA_2+A_4 \end{bmatrix}$$

2. 互换两个块行的位置

3. 用一个可逆矩阵左乘某一块行

分块矩阵的初等列变换包括：

1. 把一个块列的右 $P$ 倍加到另一个块行上，例如

   $$\begin{bmatrix} A_1 & A_2 \\ A_3 & A_4 \end{bmatrix} \xrightarrow[(1)\cdot P + (2)]{} \begin{bmatrix} A_1 & A_1 P + A_2 \\ A_3 & A_3 P+A_4 \end{bmatrix}$$

   互换两个块行的位置

2. 用一个可逆矩阵右乘某一块行

把分块单位矩阵作一次相应的分块初等行/列变换得到的矩阵叫做分块初等矩阵。分块初等矩阵左乘 $A$ ，则对 $A$ 作相应的分块初等行变换；分块初等矩阵右乘 $A$ ，则对 $A$ 作相应的分块初等列变换。

分块初等变换不改变矩阵的秩。分块初等矩阵都可逆。第一种分块初等变换不改变矩阵行列式的值。

常见分块方法

设 $B$ 的列向量组为 $\bm{\beta}_1,\bm{\beta}_2,\cdots,\bm{\beta}_n$ ，则

$$AB = A \begin{bmatrix} \bm{\beta}_1 & \bm{\beta}_2 & \cdots & \bm{\beta}_n \end{bmatrix} = \begin{bmatrix} A \bm{\beta}_1 & A \bm{\beta}_2 & \cdots & A \bm{\beta}_n \end{bmatrix}$$

设 $A$ 的列向量组为 $\bm{\alpha}_1,\bm{\alpha}_2,\cdots,\bm{\alpha}_n$ ， $\bm{x} = \left[x_1 \ x_2 \ \cdots \ x_n\right]^T$ ，则

$$A\bm{x} = \begin{bmatrix} \bm{\alpha}_1 & \bm{\alpha}_2 & \cdots & \bm{\alpha}_n \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} = \bm{\alpha}_1 x_1 + \bm{\alpha}_2 x_2 + \cdots \bm{\alpha}_n x_n$$

而后者正是某一向量在基 $\left\{\bm{\alpha}_i\right\}$ 下的线性表出，其中 $x_i$ 是坐标。

分块矩阵例题

幂等矩阵与对合矩阵

幂等矩阵和对合矩阵是两种重要的矩阵。这是由于幂等矩阵代表着投影，对合矩阵代表着对称。求证：$P$ 是幂等矩阵的充要条件是$\operatorname{rank} P + \operatorname{rank} (I-P) = n$， $S$ 是对合矩阵的充要条件是 $\operatorname{rank} (I+S) + \operatorname{rank} (I-S) = n$ 。

推论：设 $A_1,A_2,\cdots,A_m$ 为 $n$ 阶方阵，且满足 $A_1+A_2+\cdots+A_m = I$。则 $A_1,\cdots,A_m$ 都是幂等矩阵当且仅当 $\operatorname{rank} A_1 + \operatorname{rank} A_2 + \cdots + \operatorname{rank} A_m = n$ 。

矩阵乘积的行列式

利用分块矩阵的方法，求证： $\det(AB)=\det(A)\det(B)$ 。

一方面，考虑分块矩阵$\begin{pmatrix} A & O \\ I & B \end{pmatrix}$，将其按前 $n$ 行展开，则

$$\det \begin{pmatrix} A & O \\ I & B \end{pmatrix} = \det A \det B$$

另一方面，对分块矩阵$\begin{pmatrix} A & O \\ I & B \end{pmatrix}$进行分块初等变换

$$\begin{pmatrix} I & -A \\ O & I \end{pmatrix} \begin{pmatrix} A & O \\ I & B \end{pmatrix} =\begin{pmatrix} O & -AB \\ I & B \end{pmatrix}$$

不改变行列式的值。因此再对 $\begin{pmatrix} O & -AB \\ I & B \end{pmatrix}$ 前 $n$ 行展开，得

$$\begin{aligned} \det \begin{pmatrix} O & -AB \\ I & B \end{pmatrix} &= \det(-AB) \det(I) (-1)^{1+2+\cdots + n + n+1 \cdots + 2n} \\ &= (-1)^n \det (AB) (-1)^{n(2n+1)} \\ &= \det (AB) (-1)^{n(2n+2)} \\ &= \det (AB) \end{aligned}$$

重要关系

设 $A,B$ 分别是 $s\times n, n\times s$ 矩阵，求证： $\det(I_s - A B) = \det(I_n - BA)$ 。

提示：利用 $\begin{vmatrix} I_n & B \\ A & I_s \end{vmatrix}$ 。

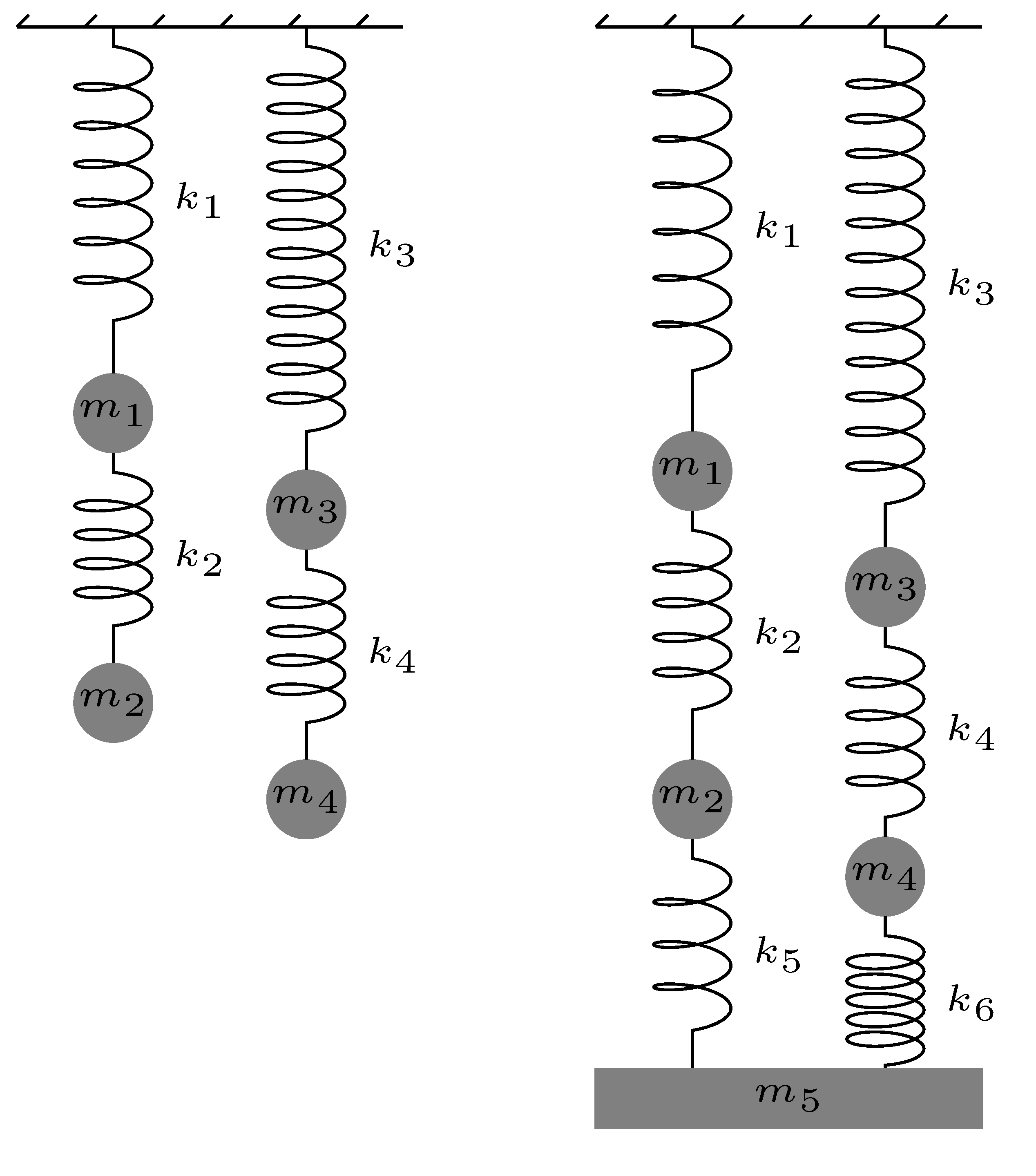
分块矩阵的力学应用

四个弹簧振子。弹簧的初始长度为 $l_1,l_2,l_3,l_4$ ，振子在稳态的最终长度为 $l_1+x_1,l_2+x_2,l_3+x_3,l_4+x_4$ 。

1. 找到矩阵 $A$ 使得 $A \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{bmatrix} = g \begin{bmatrix} m_1 \\ m_2 \\ m_3 \\ m_4 \end{bmatrix}$ 。此时 $A$ 的分块结构有什么特点？你能否从系统中直接看出原因？

2. 振子下面由劲度系数为 $k_5,k_6$ 的弹簧挂住了一个质量为 $m_5$ 的振子。找到矩阵 $A$ 使得 $A \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5 \end{bmatrix} = g \begin{bmatrix} m_1 \\ m_2 \\ m_3 \\ m_4 \\ m_5 \end{bmatrix}$ 。此时 $A$ 的分块结构是否还有以前的特点？为什么？

合同关系

数域 $\mathbb{F}$ 上两个 $n$ 级矩阵 $A$ 与 $B$ ，如果存在数域 $\mathbb{F}$ 上的一个 $n$ 级可逆矩阵 $P$ ，使得

$$P^T A P = B$$

则称 $A$ 与 $B$ 合同，记作 $A \simeq B$ 。

对称矩阵的对角化

求证：数域 $\mathbb{F}$ 上任一对称矩阵都合同于一个对角矩阵。

对于数域 $\mathbb{F}$ 上对称矩阵的级数 $n$ 作数学归纳法。

当 $n=1$ 时， $\left[a\right] \simeq \left[a\right]$ 。

假设 $n-1$ 级对称矩阵都合同于对角矩阵，现在来看 $n$ 级对称矩阵 $A=[a_{ij}]$ 。

情形1 $a_{11} \neq 0$

把 $A$ 写成分块矩阵的形式，约定小写英文字母为数字，希腊字母为列向量，大写英文字母为矩阵，有

$$A = \begin{bmatrix} a_{11} & \bm{\alpha} \\ \bm{\alpha}^T & A_1 \end{bmatrix}$$

对其作初等行列变换，使其成为分块对角矩阵

$$\begin{bmatrix} a_{11} & \bm{\alpha} \\ \bm{\alpha}^T & A_1 \end{bmatrix} \xrightarrow{(-a_{11}^{-1}\bm{\alpha} ^T)\cdot(1)+(2)} \begin{bmatrix} a_{11} & \bm{\alpha} \\ 0 & A_1-a_{11}^{-1}\bm{\alpha} ^T \bm{\alpha} \end{bmatrix} \xrightarrow[(-a_{11}^{-1}\bm{\alpha})\cdot(1)+(2)]{} \begin{bmatrix} a_{11} & 0 \\ 0 & A_1-a_{11}^{-1}\bm{\alpha} ^T \bm{\alpha} \end{bmatrix}$$

把分块初等变换的过程用分块初等矩阵表示，就是

$$\begin{bmatrix} 1 & \boldsymbol{0} \\ -a_{11}^{-1} \bm{\alpha}^T & I_{n-1} \end{bmatrix} \begin{bmatrix} a_{11} & \bm{\alpha} \\ \bm{\alpha}^T & A_1 \end{bmatrix} \begin{bmatrix} 1 & -a_{11}^{-1} \bm{\alpha} \\ \boldsymbol{0} & I_{n-1} \end{bmatrix} = \begin{bmatrix} a_{11} & 0 \\ 0 & A_1-a_{11}^{-1}\bm{\alpha} ^T \bm{\alpha} \end{bmatrix}$$

由于

$$\begin{bmatrix} 1 & -a_{11}^{-1} \bm{\alpha} \\ \boldsymbol{0} & I_{n-1} \end{bmatrix}^T = \begin{bmatrix} 1 & \boldsymbol{0} \\ -a_{11}^{-1} \bm{\alpha}^T & I_{n-1} \end{bmatrix}$$

满足合同的条件，因此

$$A \simeq \begin{bmatrix} a_{11} & 0 \\ 0 & A_1-a_{11}^{-1}\bm{\alpha} ^T \bm{\alpha} \end{bmatrix}$$

并且

$$(A_1-a_{11}^{-1}\bm{\alpha} ^T \bm{\alpha})^T = A_1^T -a_{11}^{-1}(\bm{\alpha} ^T \bm{\alpha})^T = A_1-a_{11}^{-1}\bm{\alpha} ^T \bm{\alpha}$$

这意味着 $A_2 = A_1-a_{11}^{-1}\bm{\alpha} ^T \bm{\alpha}$ 是一个 $n-1$ 级对称矩阵，于是得到 $A$ 合同于一个分块对角对称矩阵。

由归纳假设， $n-1$ 级对称矩阵合同与对角矩阵，因此存在一个可逆矩阵 $P$ ，使得 $P^T A_2 P = \operatorname{diag} \{\lambda_1,\cdots,\lambda_{n-1}\}$ ，从而

$$\begin{bmatrix} 1 & \boldsymbol{0} \\ \boldsymbol{0} & P \end{bmatrix}^T \begin{bmatrix} a_{11} & 0 \\ 0 & A_2 \end{bmatrix} \begin{bmatrix} 1 & \boldsymbol{0} \\ \boldsymbol{0} & P \end{bmatrix} = \begin{bmatrix} a_{11} & 0 \\ 0 & \operatorname{diag}\{ \lambda_i \} \end{bmatrix}$$

因此

$$A \simeq \begin{bmatrix} a_{11} & 0 \\ 0 & \operatorname{diag}\{ \lambda_i \} \end{bmatrix}$$

情形2 $a_{11} = 0$ ，存在 $a_{ii}=0$

把 $A$ 的第 $1,i$ 行互换，再把第 $1,i$ 列互换，回到情形1。

情形3 $a_{11} = a_{22} = \cdots = a_{nn} = 0$ ，存在 $a_{ij}\neq 0 \ (i \neq j)$

把 $A$ 的第 $j$ 行加到第 $i$ 行上，再把所得矩阵的第 $j$ 列加到第 $i$ 列上，得到的矩阵 $B$ 的第 $(i,i)$ 元为 $2a_{ij}$ ，回到情形2。

情形4 $A=O$

这是平庸的。

秩不等式

秩的概念

秩的定义是矩阵列向量的极大线性无关组中向量的个数。

秩的意义在于，它描述了在矩阵的作用下，有多少信息维度仍然保留着。这是通过解空间维数定理（代数角度）或秩加零度定理（几何角度）来实现的。即所谓

$$\operatorname{dim}W + \operatorname{rank} A = n$$

$$\operatorname{null} \mathscr{A} + \operatorname{rank} \mathscr{A} = n$$

秩是相抵关系的完全不变量。

秩不等式

秩不等式有很多，列举一些常见而有用的：

$$\operatorname{rank} (A|B) \le \operatorname{rank} A + \operatorname{rank} B$$

$$\operatorname{rank} (A|B) \ge \max\left\{\operatorname{rank} A , \operatorname{rank} B\right\}$$

$$\operatorname{rank} \begin{bmatrix} A & O\\ O & B \end{bmatrix} = \operatorname{rank} A + \operatorname{rank} B$$

$$\operatorname{rank} \begin{bmatrix} A & C\\ O & B \end{bmatrix} \ge \operatorname{rank} A + \operatorname{rank} B$$

$$\boxed{\operatorname{rank} (AB) \ge \operatorname{rank} A + \operatorname{rank} B - n}$$

$$\operatorname{rank} (A+B) \le \operatorname{rank} A + \operatorname{rank} B$$

其中带方框的式子称为Sylvester秩不等式。

例题

Frobenius 秩不等式

设 $A,B,C$ 分别是 $s\times n, n \times m, m \times t$ ，求证：

$$\operatorname{rank}(ABC) \ge \operatorname{rank}(AB) + \operatorname{rank}(BC) - \operatorname{rank}(B)$$

幂等矩阵与对合矩阵

求证： $P$ 是幂等矩阵的必要条件是 $\operatorname{rank} P + \operatorname{rank} (I-P) = n$， $S$ 是对合矩阵的必要条件是 $\operatorname{rank} (I+S) + \operatorname{rank} (I-S) = 0$ 。

首先转化为等价命题，若 $P$ 是幂等矩阵，则有

$$P^2 = P \iff P^2 - P = O \iff \operatorname{rank} (P^2 - P) = 0$$

由 Sylvester 秩不等式，有

$$\operatorname{rank} P + \operatorname{rank} (I-P) \le \operatorname{rank} (P^2 - P) + n = n$$

另一方面，由公式六，有

$$\operatorname{rank} P + \operatorname{rank} (I-P) \ge \operatorname{rank}(P+I-P) = n$$

因此只能有 $\operatorname{rank} P + \operatorname{rank} (I-P)=n$ 。

对合矩阵请读者自证。

秩一分解

求证：秩为 $r$ 的矩阵可以表示为 $r$ 个秩为 $1$ 的矩阵之和。但是不能表为少于 $r$ 个秩为 $1$ 的矩阵之和。

假设 $A$ 是秩为 $r$ 的矩阵，则由相抵标准型理论，可以得到

$$A=P \begin{bmatrix} I_r & O\\ O & O \end{bmatrix} Q$$

因此

$$A=\sum_{i=1}^r P E_{ii} Q$$

其中 $E_{ii}$ 表示第 $i$ 行第 $i$ 列为1，其他位置均为0的矩阵。且显然有

$$\operatorname{rank} (P E_{ii} Q) =1$$

现在假设 $A=A_1+A_2+\cdots+A_s$ ， $s<r$ 且 $\operatorname{rank} A_i = 1$ 。由公式六知

$$\operatorname{rank} A = \operatorname{rank} (A_1+A_2+\cdots+A_s) \le \sum_i^s \operatorname{rank} A_i = s < r$$

矛盾，故假设不成立。

结语

本节课的主要内容是分块矩阵和秩不等式。

分块矩阵的要诀在于通过分块初等变换把一些子块化为零矩阵，从而简化问题。秩不等式的要诀在于想清楚不等式背后的意义，还原为极大线性无关组的构成来考虑。

这节内容几乎纯粹是数学技巧，其几何意义和物理意义并不明显。《庄子》有言曰：“所好者道也，进乎技矣”，希望同学们以这种态度学习线性代数。