这篇文章是微分流形简介,主要目标是为广义相对论的学习服务。参考的教材为梁灿彬的《微分几何与广义相对论》和梅加强的《流形与几何初步》,分别是物理系和数学系的教材。这篇文章写作时,惊闻梁灿彬老师去世,一时间百感交集。沉痛悼念之余,希望能把知识传递下去,不负梁老师的教学精神。
设 M M M A 2 A_2 A 2 T 2 T_2 T 2 M M M { U α } α ∈ Γ \{U_\alpha\}_{\alpha \in \Gamma} { U α } α ∈ Γ φ α : U α → R n \varphi_\alpha : U_\alpha \to \mathbb{R}^n φ α : U α → R n
φ α : U α → φ α ( U α ) ⊂ R n \varphi_\alpha : U_\alpha \to \varphi_\alpha(U_\alpha) \subset \mathbb{R}^n φ α : U α → φ α ( U α ) ⊂ R n U α U_\alpha U α φ α ( U α ) \varphi_\alpha(U_\alpha) φ α ( U α )
当 U α ∩ U β ≠ ∅ U_\alpha \cap U_\beta \neq \varnothing U α ∩ U β = ∅
φ β ∘ φ α − 1 : R n → R n φ α ( U α ∩ U β ) ↦ φ β ( U α ∩ U β ) \begin{aligned}
\varphi_{\beta} \circ \varphi_{\alpha}^{-1}: \mathbb{R}^n &\to \mathbb{R}^n \\
\varphi_{\alpha}\left(U_{\alpha} \cap U_{\beta}\right) &\mapsto \varphi_{\beta}\left(U_{\alpha} \cap U_{\beta}\right)
\end{aligned}
φ β ∘ φ α − 1 : R n φ α ( U α ∩ U β ) → R n ↦ φ β ( U α ∩ U β )
是 C r C^r C r r r r
则当 r = 0 r=0 r = 0 M M M 拓扑流形 ,当 1 ≤ r < ∞ 1\le r<\infty 1 ≤ r < ∞ M M M C r C^r C r 微分流形 ,当 r = ∞ r = \infty r = ∞ M M M 光滑流形 。
公式
定义
{ U α } \{U_\alpha\} { U α } 流形 M M M
( U α , φ α ) (U_\alpha,\varphi_\alpha) ( U α , φ α ) 局部坐标系 / 坐标卡
U α U_\alpha U α 局部坐标邻域
φ α \varphi_\alpha φ α 局部坐标映射
p ∈ M p \in M p ∈ M 流形上的点
设 φ α ( p ) = [ x 1 ( p ) , x 2 ( p ) , ⋯ , x n ( p ) ] \varphi_\alpha(p) = \left[ x^1 (p),x^2 (p),\cdots, x^n(p) \right] φ α ( p ) = [ x 1 ( p ) , x 2 ( p ) , ⋯ , x n ( p ) ] x i : U α → R x^i: U_\alpha \to R x i : U α → R ( U α , φ α ) (U_\alpha,\varphi_\alpha) ( U α , φ α ) i i i { x i } \{x^i\} { x i } p p p 局部坐标 。若 p ∈ U α ∩ U β p \in U_\alpha \cap U_\beta p ∈ U α ∩ U β p p p ( U α , φ α ) (U_\alpha,\varphi_\alpha) ( U α , φ α ) ( U β , φ β ) (U_\beta,\varphi_\beta) ( U β , φ β ) { x i } \{x^i\} { x i } { x ′ i } \{x^{\prime i}\} { x ′ i } φ β ∘ φ α − 1 \varphi_{\beta} \circ \varphi_{\alpha}^{-1} φ β ∘ φ α − 1 坐标转换 映射。若此坐标转换映射是 C r C^r C r ( U α , φ α ) (U_\alpha,\varphi_\alpha) ( U α , φ α ) ( U β , φ β ) (U_\beta,\varphi_\beta) ( U β , φ β ) 相容 的。
例:设 M M M R n \mathbb{R}^n R n U 1 = R n , φ 1 = i d U_1 = \mathbb{R}^n, \varphi_1 = \mathrm{id} U 1 = R n , φ 1 = i d R n \mathbb{R}^n R n
微分结构 对于任何一个坐标卡 ( U α , φ α ) (U_\alpha,\varphi_\alpha) ( U α , φ α ) D \mathscr{D} D D \mathscr{D} D ( U , φ ) (U,\varphi) ( U , φ ) D \mathscr{D} D D \mathscr{D} D M M M C r C^r C r
换言之,装备有 C r C^r C r
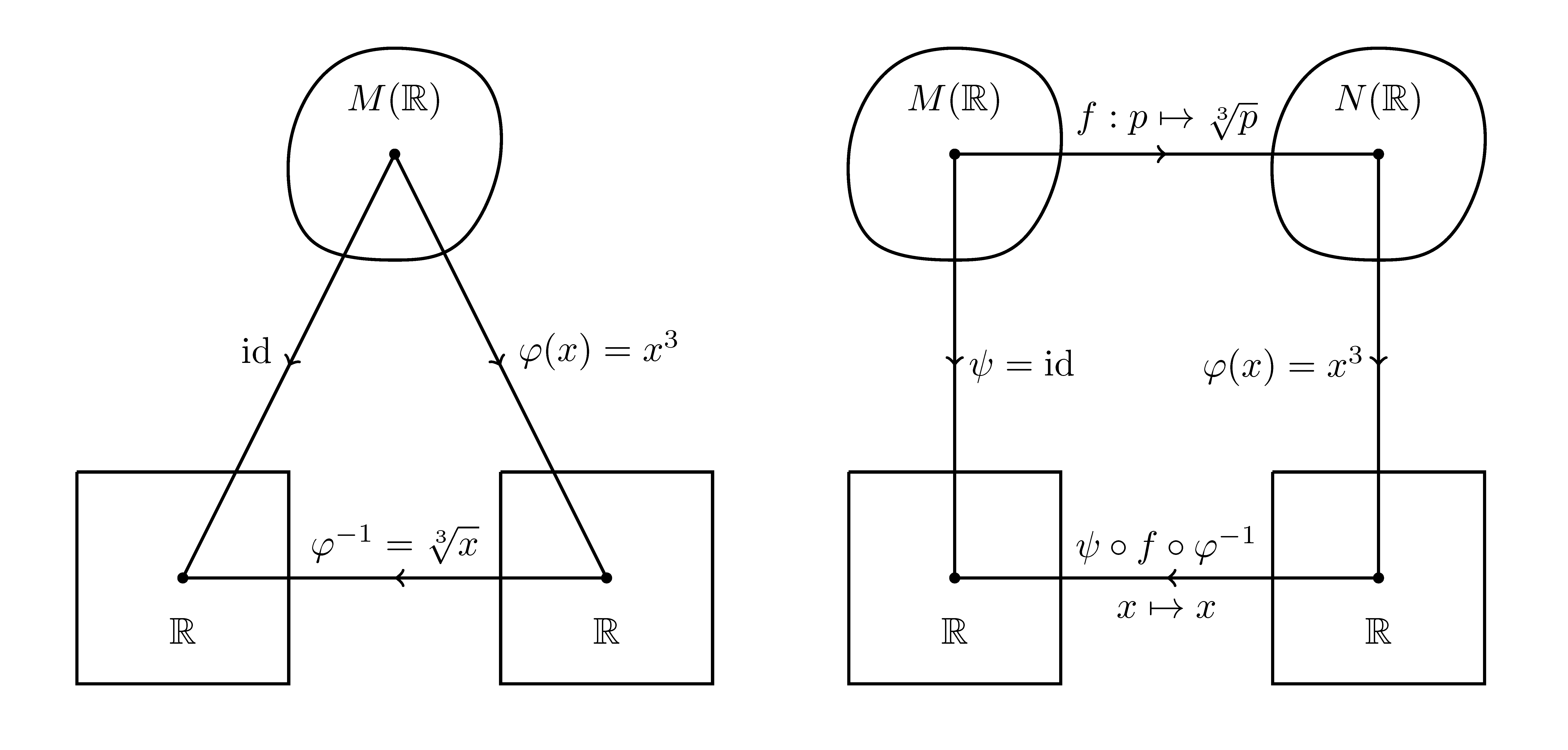
考虑标准拓扑空间 R \mathbb{R} R ( R , i d ) (\R , \mathrm{id}) ( R , i d ) φ : R → R , φ ( x ) = x 3 \varphi: \R \to \R, \varphi(x) = x^3 φ : R → R , φ ( x ) = x 3 ( R , φ ) (\R , \varphi) ( R , φ ) M M M R \mathbb{R} R ( R , i d ) (\R , \mathrm{id}) ( R , i d ) ( R , φ ) (\R , \varphi) ( R , φ ) φ − 1 ( x ) = x 3 \varphi^{-1}(x) = \sqrt[3]{x} φ − 1 ( x ) = 3 x x = 0 x=0 x = 0
Cr映射 设 C k C^k C k M M M N N N { ( U α , φ α ) } \{(U_\alpha,\varphi_\alpha)\} { ( U α , φ α ) } { ( V β , ψ β ) } \{(V_\beta,\psi_\beta)\} { ( V β , ψ β ) } f : M → N f:M \to N f : M → N
任给 p ∈ M p \in M p ∈ M f ( p ) ∈ N f(p) \in N f ( p ) ∈ N ( V , ψ ) (V,\psi) ( V , ψ ) p p p ( U , φ ) (U,\varphi) ( U , φ ) f ( U ) ⊂ V f(U) \subset V f ( U ) ⊂ V
复合映射 ψ ∘ f ∘ φ − 1 : φ ( U ) → ψ ( V ) \psi \circ f \circ \varphi^{-1}: \varphi(U) \to \psi (V) ψ ∘ f ∘ φ − 1 : φ ( U ) → ψ ( V ) C r C^r C r r ≤ k r \le k r ≤ k
则称 f f f M , N M,N M , N C r C^r C r
微分同胚 设流形 M M M N N N C r C^r C r f : M → N f:M \to N f : M → N f f f f − 1 f^{-1} f − 1 C r C^r C r f f f C r C^r C r f f f
当我们不加申明的时候,光滑流形之间的微分同胚指的是光滑的微分同胚。我们不区分微分同胚的流形。特别地,在同一个拓扑流形上,如果两个微分结构定义出的微分流形是微分同胚的,则我们称这两个微分结构等价,我们不区分等价的微分结构。
我们仍然用微分结构一节中的例子理清概念辨析区别。我们将装备 ( R , i d ) (\R , \mathrm{id}) ( R , i d ) R \mathbb{R} R M M M φ : R → R , φ ( x ) = x 3 \varphi: \R \to \R, \varphi(x) = x^3 φ : R → R , φ ( x ) = x 3 ( R , φ ) (\R , \varphi) ( R , φ ) R \mathbb{R} R N N N M M M N N N f : p ↦ p 3 f: p \mapsto \sqrt[3]{p} f : p ↦ 3 p
读者可能感到疑惑,微分同胚的映射不应当是光滑的吗?我们刚根据 x 3 \sqrt[3]{x} 3 x C 1 C^1 C 1 ( R , i d ) (\R , \mathrm{id}) ( R , i d ) ( R , φ ) (\R , \varphi) ( R , φ ) R \mathbb{R} R i d , φ \mathrm{id},\varphi i d , φ ( R , i d ) (\R , \mathrm{id}) ( R , i d ) ( R , φ ) (\R , \varphi) ( R , φ ) C r C^r C r C r C^r C r C r C^r C r
如图所示,坐标转换映射 ψ ∘ f ∘ φ − 1 : R → R \psi \circ f \circ \varphi^{-1}: \mathbb{R} \to \mathbb{R} ψ ∘ f ∘ φ − 1 : R → R ψ ∘ f ∘ φ − 1 : x ↦ x \psi \circ f \circ \varphi^{-1}: x \mapsto x ψ ∘ f ∘ φ − 1 : x ↦ x C ∞ C^\infty C ∞
设 M M M M M M { ( U α , φ α ) } \{(U_\alpha,\varphi_\alpha)\} { ( U α , φ α ) } U α ∩ U β ≠ ∅ U_\alpha \cap U_\beta \neq \varnothing U α ∩ U β = ∅ det J ( φ β ∘ φ α − 1 ) > 0 \operatorname{det} J\left(\varphi_{\beta} \circ \varphi_{\alpha}^{-1}\right)>0 d e t J ( φ β ∘ φ α − 1 ) > 0 J J J M M M { ( U α , φ α ) } \{(U_\alpha,\varphi_\alpha)\} { ( U α , φ α ) } M M M
函数/标量场 映射 f : M → R f: M \to \R f : M → R M M M f f f C ∞ C^\infty C ∞ f f f M M M C ∞ ( M ) C^\infty (M) C ∞ ( M )
/* 注:这里 f f f M M M R \mathbb{R} R
切向量 设 p ∈ M p \in M p ∈ M X p : C ∞ ( M ) → R X_{p}: C^{\infty}(M) \rightarrow \mathbb{R} X p : C ∞ ( M ) → R
X p X_p X p ∀ f , g ∈ C ∞ ( M ) \forall f, g \in C^{\infty}(M) ∀ f , g ∈ C ∞ ( M ) X p ( f g ) = f ( p ) X p g + g ( p ) X p f X_{p}(f g)=f(p) X_{p} g+g(p) X_{p} f X p ( f g ) = f ( p ) X p g + g ( p ) X p f
则称 X p X_p X p M M M p p p
切空间 切向量的全体组成的向量空间称为 p p p T p ( M ) T_p(M) T p ( M )
根据定义,切向量作用在常值函数上为零。切向量作用在函数上就如同多元函数沿一个方向求方向导数。
切空间的基 设 ( U , φ ) (U,\varphi) ( U , φ ) p p p f : M → R f: M \to \R f : M → R φ : M → R n \varphi:M \to \mathbb{R}^n φ : M → R n
f ∘ φ − 1 : R n → R φ ( p ) ↦ f ( p ) \begin{aligned}
f \circ \varphi^{-1} : \mathbb{R}^n &\to \mathbb{R} \\
\varphi(p) &\mapsto f(p)
\end{aligned}
f ∘ φ − 1 : R n φ ( p ) → R ↦ f ( p )
正如多元函数的方向导数可以分解在梯度上,在 p p p n n n ∂ ∂ x μ ∣ p \left.\dfrac{\partial}{\partial x^{\mu}}\right|_{p} ∂ x μ ∂ ∣ ∣ ∣ ∣ ∣ p
∂ ∂ x μ ∣ p f = ∂ f ∘ φ − 1 ∂ x μ ( φ ( p ) ) \left.\frac{\partial}{\partial x^{\mu}}\right|_{p} f=\frac{\partial f \circ \varphi^{-1}}{\partial x^{\mu}}(\varphi(p))
∂ x μ ∂ ∣ ∣ ∣ ∣ ∣ p f = ∂ x μ ∂ f ∘ φ − 1 ( φ ( p ) )
数学上可以证明,有
X p = ∑ μ = 1 n ( X p x μ ) ∂ ∂ x μ ∣ p X_{p}=\left.\sum_{\mu=1}^{n}\left(X_{p} x^{\mu}\right) \frac{\partial}{\partial x^{\mu}}\right|_{p}
X p = μ = 1 ∑ n ( X p x μ ) ∂ x μ ∂ ∣ ∣ ∣ ∣ ∣ ∣ p
其中 X p x μ X_{p} x^{\mu} X p x μ X p X_p X p μ \mu μ x μ x^\mu x μ x μ x^\mu x μ M M M R \R R
因此切向量 ∂ ∂ x μ ∣ p \left.\dfrac{\partial}{\partial x^{\mu}}\right|_{p} ∂ x μ ∂ ∣ ∣ ∣ ∣ ∣ p p p p T p ( M ) T_p(M) T p ( M ) p p p n n n
切丛 流形 M M M p p p M M M T M TM T M
T M = ⋃ p ∈ M T p M T M=\bigcup_{p \in M} T_{p} M
T M = p ∈ M ⋃ T p M
或者说,T M TM T M M M M
定义投影映射 π : T M → M \pi: TM \to M π : T M → M
π : T M → M X p ↦ p \begin{aligned}
\pi: TM &\to M \\
X_p &\mapsto p
\end{aligned}
π : T M X p → M ↦ p
则 π \pi π 投影 。
设 ( U , φ ) (U,\varphi) ( U , φ ) M M M ψ \psi ψ
ψ : π − 1 ( U ) = ⋃ p ∈ U T p M → U × R n X p ↦ ( p , X p ( x 1 ) , X p ( x 2 ) , ⋯ , X p ( x n ) ) \begin{aligned}
\psi: \pi^{-1}(U)=\bigcup_{p \in U} T_{p} M & \rightarrow U \times \mathbb{R}^{n} \\
X_{p} & \mapsto\left(p, X_{p}\left(x^{1}\right), X_{p}\left(x^{2}\right), \cdots, X_{p}\left(x^{n}\right)\right)
\end{aligned}
ψ : π − 1 ( U ) = p ∈ U ⋃ T p M X p → U × R n ↦ ( p , X p ( x 1 ) , X p ( x 2 ) , ⋯ , X p ( x n ) )
可以证明,T M TM T M 2 n 2n 2 n { ( π − 1 ( U α ) , ( φ α , i d ) ∘ ψ α ) ) } \left.\left\{\left(\pi^{-1}\left(U_{\alpha}\right),\left(\varphi_{\alpha}, \mathrm{id}\right) \circ \psi_{\alpha}\right)\right)\right\} { ( π − 1 ( U α ) , ( φ α , i d ) ∘ ψ α ) ) } n n n p p p n n n p p p
( φ α , i d ) ∘ ψ α : π − 1 ( U ) → R 2 n X p ↦ ( x 1 ( p ) , x 2 ( p ) , ⋯ , x n ( p ) , X p ( x 1 ) , X p ( x 2 ) , ⋯ , X p ( x n ) ) \begin{aligned}
\left(\varphi_{\alpha}, \mathrm{id}\right) \circ \psi_{\alpha}: \pi^{-1}(U) & \rightarrow \mathbb{R}^{2n} \\
X_p & \mapsto\left( x^1 (p),x^2 (p),\cdots, x^n(p), X_{p}\left(x^{1}\right), X_{p}\left(x^{2}\right), \cdots, X_{p} \left(x^{n}\right)\right)
\end{aligned}
( φ α , i d ) ∘ ψ α : π − 1 ( U ) X p → R 2 n ↦ ( x 1 ( p ) , x 2 ( p ) , ⋯ , x n ( p ) , X p ( x 1 ) , X p ( x 2 ) , ⋯ , X p ( x n ) )
其中 φ \varphi φ i d \mathrm{id} i d
切向量场 设 X : M → T M X : M \to TM X : M → T M C r C^r C r π ∘ X = i d M \pi \circ X = \mathrm{id}_M π ∘ X = i d M M M M X X X M M M C r C^r C r
上述定义过于抽象,通俗来说,过流形 M M M p p p X X X p p p M M M
流形 M M M X ( M ) \mathfrak{X}(M) X ( M ) Γ ( T M ) \varGamma(TM) Γ ( T M )
切向量场 X X X f f f X f Xf X f p ∈ M p \in M p ∈ M
X f ∣ p = X p f , ∀ p ∈ M X f |_p = X_p f , \quad \forall p \in M
X f ∣ p = X p f , ∀ p ∈ M
/* 注:X X X M M M T M TM T M X X X C ∞ ( M ) C^\infty(M) C ∞ ( M ) C ∞ ( M ) C^\infty(M) C ∞ ( M )
函数 f f f X X X f X fX f X p ∈ M p \in M p ∈ M
f X ∣ p = f ( p ) X p , ∀ p ∈ M fX|_p = f(p) X_p , \quad \forall p \in M
f X ∣ p = f ( p ) X p , ∀ p ∈ M
切映射 设 f : M → N f: M \to N f : M → N p ∈ M p \in M p ∈ M X p X_p X p f ( p ) f(p) f ( p ) f ∗ p ( X p ) f_{*p}(X_p) f ∗ p ( X p )
f ∗ p ( X p ) g = X p ( g ∘ f ) ∀ g ∈ C ∞ ( N ) f_{*p} (X_p) g = X_p (g \circ f) \qquad \forall g \in C^\infty(N)
f ∗ p ( X p ) g = X p ( g ∘ f ) ∀ g ∈ C ∞ ( N )
这样我们就定义了线性映射 f ∗ p : T p M → T f ( p ) N f_{*p} : T_p M \to T_{f(p)} N f ∗ p : T p M → T f ( p ) N f f f p p p
/* 注:这种定义方式有点像线性空间到双重对偶空间的典范同构 */
需要说明,g ∘ f g \circ f g ∘ f M → R M \to \mathbb{R} M → R M M M X p ( g ∘ f ) ∈ R X_p (g \circ f) \in \mathbb{R} X p ( g ∘ f ) ∈ R
切微分/余切向量 特殊地,若取切映射中的 N N N R \mathbb{R} R f ∗ p : T p M → T f ( p ) R f_{*p} : T_p M \to T_{f(p)}\mathbb{R} f ∗ p : T p M → T f ( p ) R R \R R T f ( p ) R T_{f(p)}\mathbb{R} T f ( p ) R R \mathbb{R} R g g g i d \mathrm{id} i d f ∗ p f_{*p} f ∗ p M M M f f f p p p d f ∣ p \mathrm{d} f |_p d f ∣ p f f f p p p
d f ∣ p : T p M → R X p ↦ d f ∣ p ( X p ) = X p ( i d ∘ f ) = X p ( f ) \begin{aligned}
\mathrm{d} f|_p : T_p M &\to \R \\
X_p &\mapsto \mathrm{d} f |_p(X_p)=X_p ( \mathrm{id}\circ f) = X_p ( f)
\end{aligned}
d f ∣ p : T p M X p → R ↦ d f ∣ p ( X p ) = X p ( i d ∘ f ) = X p ( f )
/* 注:这种定义方式就是线性空间到双重对偶空间的典范同构 */ f f f M M M x α i ( i = 1 , 2 , ⋯ , dim M ) x_\alpha^i\,(i=1,2,\cdots,\dim M) x α i ( i = 1 , 2 , ⋯ , dim M ) d x α i ∣ p ( ∂ ∂ x α j ∣ p ) = ∂ x α i ∂ x α j ∣ p ≡ δ j i \mathrm{d} x_\alpha^i|_p \left( \left.\dfrac{\partial}{\partial x^j_{\alpha}}\right|_{p}\right) = \left.\dfrac{\partial x_\alpha^i}{\partial x^j_{\alpha}}\right|_{p} \equiv \delta^i_j d x α i ∣ p ( ∂ x α j ∂ ∣ ∣ ∣ ∣ ∣ p ) = ∂ x α j ∂ x α i ∣ ∣ ∣ ∣ ∣ p ≡ δ j i
余切空间 由于切微分/余切向量的作用方法被定义成 X p X_p X p X p X_p X p T p ∗ M T_p^* M T p ∗ M
T p ∗ M = { d f p ∣ f ∈ C ∞ ( M ) } T_p^* M = \left\{ \mathrm{d}f_p \mid f \in C^\infty (M)\right\}
T p ∗ M = { d f p ∣ f ∈ C ∞ ( M ) }
与此同时,T p ∗ M T_p^* M T p ∗ M T p M T_p M T p M T p ∗ M T_p^* M T p ∗ M T p M → R T_p M \to \R T p M → R d x α i ∣ p ( ∂ ∂ x α j ∣ p ) = ∂ x α i ∂ x α j ∣ p ≡ δ j i \mathrm{d} x_\alpha^i|_p \left( \left.\dfrac{\partial}{\partial x^j_{\alpha}}\right|_{p}\right) = \left.\dfrac{\partial x_\alpha^i}{\partial x^j_{\alpha}}\right|_{p} \equiv \delta^i_j d x α i ∣ p ( ∂ x α j ∂ ∣ ∣ ∣ ∣ ∣ p ) = ∂ x α j ∂ x α i ∣ ∣ ∣ ∣ ∣ p ≡ δ j i p p p d x α i ∣ p ( i = 1 , ⋯ , n ) \mathrm{d} x_\alpha^i|_p \ (i=1,\cdots,n) d x α i ∣ p ( i = 1 , ⋯ , n )
T p ∗ M = span { d x α 1 ∣ p , d x α 2 ∣ p , ⋯ , d x α n ∣ p } T_p^* M = \operatorname{span} \{ \mathrm{d} x_\alpha^1|_p , \mathrm{d} x_\alpha^2|_p , \cdots, \mathrm{d} x_\alpha^n|_p\}
T p ∗ M = s p a n { d x α 1 ∣ p , d x α 2 ∣ p , ⋯ , d x α n ∣ p }
且 T p ∗ M T_p^* M T p ∗ M ω ( p ) \omega(p) ω ( p )
ω ( p ) = ∑ i = 1 n a i d x α i ∣ p \omega(p) = \sum_{i=1}^n a_i \mathrm{d} x_\alpha^i|_p
ω ( p ) = i = 1 ∑ n a i d x α i ∣ p
余切丛 流形 M M M p p p M M M
T ∗ M = ⋃ p ∈ M T p ∗ M T^* M=\bigcup_{p \in M} T_{p}^* M
T ∗ M = p ∈ M ⋃ T p ∗ M
T ∗ M T^* M T ∗ M
回顾切丛和余切丛的结构,尤其是微分同胚
ψ : π − 1 ( U ) = ⋃ p ∈ U T p M → U × R n X p ↦ ( p , X p ( x 1 ) , X p ( x 2 ) , ⋯ , X p ( x n ) ) \begin{aligned}
\psi: \pi^{-1}(U)=\bigcup_{p \in U} T_{p} M & \rightarrow U \times \mathbb{R}^{n} \\
X_{p} & \mapsto\left(p, X_{p}\left(x^{1}\right), X_{p}\left(x^{2}\right), \cdots, X_{p}\left(x^{n}\right)\right)
\end{aligned}
ψ : π − 1 ( U ) = p ∈ U ⋃ T p M X p → U × R n ↦ ( p , X p ( x 1 ) , X p ( x 2 ) , ⋯ , X p ( x n ) )
可以发现在流形 M M M U U U U U U R n \mathbb{R}^n R n
切丛局部上是乘积空间,且乘积空间的第二个分量为线性空间
切丛的局部坐标转换映射保持第二个分量的线性性
由此可以将这种微分流形进行推广,即向量丛和纤维丛。
向量丛 设 E , M E,M E , M π : E → M \pi : E \to M π : E → M M M M { U α } \{U_\alpha\} { U α } ψ α : π − 1 ( U α ) → U α × R n \psi_{\alpha}: \pi^{-1}\left(U_{\alpha}\right) \rightarrow U_{\alpha} \times \mathbb{R}^{n} ψ α : π − 1 ( U α ) → U α × R n
ψ ( π − 1 ( p ) ) = { p } × R n , ∀ p ∈ U α \psi\left(\pi^{-1}(p)\right)=\{p\} \times \mathbb{R}^{n}, \quad \forall p \in U_{\alpha} ψ ( π − 1 ( p ) ) = { p } × R n , ∀ p ∈ U α
当 U α ∩ U β ≠ ∅ U_\alpha \cap U_\beta \neq \varnothing U α ∩ U β = ∅ g β α : U α ⋂ U β → G L ( n , R ) g_{\beta \alpha}: U_{\alpha} \bigcap U_{\beta} \rightarrow GL(n,\mathbb{R}) g β α : U α ⋂ U β → G L ( n , R )
ψ β ∘ ψ α − 1 ( p , v ) = ( p , g β α ( p ) v ) , ∀ p ∈ U α ∩ U β , v ∈ R n \psi_{\beta} \circ \psi_{\alpha}^{-1}(p, v)=\left(p, g_{\beta \alpha}(p) v\right), \quad \forall p \in U_{\alpha} \cap U_{\beta}, v \in \mathbb{R}^{n}
ψ β ∘ ψ α − 1 ( p , v ) = ( p , g β α ( p ) v ) , ∀ p ∈ U α ∩ U β , v ∈ R n
则称 E E E M M M 向量丛 ,n n n π \pi π E E E M M M ψ α \psi_\alpha ψ α π − 1 ( p ) = E p ≅ R n \pi^{-1}(p)=E_{p} \cong \mathbb{R}^n π − 1 ( p ) = E p ≅ R n p p p g β α g_{\beta \alpha} g β α g β α g_{\beta \alpha} g β α
向量丛的截面/向量场 设 E E E M M M π : E → M \pi : E \to M π : E → M C r C^r C r σ : M → E \sigma: M \to E σ : M → E π ∘ σ = i d M \pi \circ \sigma = \mathrm{id}_M π ∘ σ = i d M σ ( p ) ∈ π − 1 ( p ) \sigma(p) \in \pi^{-1}(p) σ ( p ) ∈ π − 1 ( p ) σ \sigma σ E E E C r C^r C r 向量场 。
流形 M M M E E E M M M Γ ( M ; E ) \varGamma(M;E) Γ ( M ; E )
纤维丛 设 π : E → M \pi : E \to M π : E → M F F F G G G F F F M M M { U α } α ∈ Γ \{U_\alpha\}_{\alpha \in \Gamma} { U α } α ∈ Γ ψ α : π − 1 ( U α ) → U α × F \psi_{\alpha}: \pi^{-1}\left(U_{\alpha}\right) \rightarrow U_{\alpha} \times F ψ α : π − 1 ( U α ) → U α × F
ψ ( π − 1 ( p ) ) = { p } × F , ∀ p ∈ U α \psi\left(\pi^{-1}(p)\right)=\{p\} \times F, \quad \forall p \in U_{\alpha} ψ ( π − 1 ( p ) ) = { p } × F , ∀ p ∈ U α
当 U α ∩ U β ≠ ∅ U_\alpha \cap U_\beta \neq \varnothing U α ∩ U β = ∅ g β α : U α ⋂ U β → G g_{\beta \alpha}: U_{\alpha} \bigcap U_{\beta} \rightarrow G g β α : U α ⋂ U β → G
ψ β ∘ ψ α − 1 ( p , f ) = ( p , g β α ( p ) f ) , ∀ p ∈ U α ∩ U β , f ∈ F \psi_{\beta} \circ \psi_{\alpha}^{-1}(p, f)=\left(p, g_{\beta \alpha}(p) f\right), \quad \forall p \in U_{\alpha} \cap U_{\beta}, f \in F
ψ β ∘ ψ α − 1 ( p , f ) = ( p , g β α ( p ) f ) , ∀ p ∈ U α ∩ U β , f ∈ F
则称 E E E M M M 纤维丛 ,π \pi π 丛投影 ,F F F 纤维 ,E E E M M M 总空间 和底空间 ,G G G 结构群 ,ψ α \psi_\alpha ψ α 局部平凡化 ,π − 1 ( p ) = E p \pi^{-1}(p)=E_{p} π − 1 ( p ) = E p p p p 纤维 ,并与 F F F g β α g_{\beta \alpha} g β α
截面 设 E E E M M M π : E → M \pi : E \to M π : E → M C r C^r C r σ : M → E \sigma: M \to E σ : M → E π ∘ σ = i d M \pi \circ \sigma = \mathrm{id}_M π ∘ σ = i d M σ ( p ) ∈ π − 1 ( p ) \sigma(p) \in \pi^{-1}(p) σ ( p ) ∈ π − 1 ( p ) σ \sigma σ E E E C r C^r C r
定理:由场张量可以唯一确定张量场,由张量场也可以唯一确定场张量。