这篇文章是Lie导数与Killing场,主要目标是为广义相对论的学习服务。参考的教材为梁灿彬的《微分几何与广义相对论》、陈斌的《广义相对论》梅加强的《流形与几何初步》,分别是物理系和数学系的教材。最近 A-SOUL 给我的打击很大,博客停更了一段时间。希望广义相对论的学习能帮助调整状态吧。
函数的拉回映射 设 ϕ : M → N \phi: M \to N ϕ : M → N ϕ ∗ : C ∞ ( N ) → C ∞ ( N ) \phi^*:C^\infty(N) \to C^\infty(N) ϕ ∗ : C ∞ ( N ) → C ∞ ( N )
ϕ ∗ f = f ∘ ϕ ∀ f ∈ C ∞ ( N ) \phi^* f = f \circ \phi \qquad \forall f \in C^\infty (N)
ϕ ∗ f = f ∘ ϕ ∀ f ∈ C ∞ ( N )
则 ϕ ∗ f ∈ C ∞ ( M ) \phi^* f \in C^\infty(M) ϕ ∗ f ∈ C ∞ ( M ) M M M f f f 拉回映射 。
形象地看,ϕ ∗ \phi_* ϕ ∗ N N N M M M ϕ \phi ϕ ϕ \phi ϕ M M M N N N ϕ ∗ \phi^* ϕ ∗ N N N M M M
拉回映射具有以下性质:
ϕ ∗ ( α f + β g ) = α ϕ ∗ ( f ) + β ϕ ∗ ( g ) ∀ f , g ∈ C ∞ ( N ) , ∀ α , β ∈ R \phi^{*}(\alpha f+\beta g)=\alpha \phi^{*}(f)+\beta \phi^{*}(g) \qquad \forall f, g \in C^\infty(N), \forall\alpha, \beta \in \mathbb{R}
ϕ ∗ ( α f + β g ) = α ϕ ∗ ( f ) + β ϕ ∗ ( g ) ∀ f , g ∈ C ∞ ( N ) , ∀ α , β ∈ R
ϕ ∗ ( f g ) = ϕ ∗ ( f ) ϕ ∗ ( g ) ∀ f , g ∈ C ∞ ( N ) \phi^{*}(f g)=\phi^{*}(f) \phi^{*}(g) \qquad \forall f, g \in C^\infty(N)
ϕ ∗ ( f g ) = ϕ ∗ ( f ) ϕ ∗ ( g ) ∀ f , g ∈ C ∞ ( N )
函数的推前映射 函数无法定义推前映射,原因在于流形间的映射 ϕ : M → N \phi: M \to N ϕ : M → N ϕ ∗ f = f ∘ ϕ − 1 \phi_* f = f \circ\phi^{-1} ϕ ∗ f = f ∘ ϕ − 1
向量场的推前映射 设 ϕ : M → N \phi: M \to N ϕ : M → N ϕ ∗ : T p M → T f ( p ) N \phi_*:T_p M \to T_{f(p)}N ϕ ∗ : T p M → T f ( p ) N p ∈ M p \in M p ∈ M X p X_p X p f ( p ) ∈ N f(p)\in N f ( p ) ∈ N ϕ ∗ X p \phi_*X_p ϕ ∗ X p
( ϕ ∗ X p ) ( f ) = X p ( f ∘ ϕ ) = X p ( ϕ ∗ f ) ∀ f ∈ C ∞ ( N ) (\phi_{*} X_p) (f) = X_p (f \circ \phi) = X_p (\phi^* f)\qquad \forall f \in C^\infty(N)
( ϕ ∗ X p ) ( f ) = X p ( f ∘ ϕ ) = X p ( ϕ ∗ f ) ∀ f ∈ C ∞ ( N )
则 ϕ ∗ X p \phi_{*} X_p ϕ ∗ X p N N N X p X_p X p 推前映射 ,也叫切映射 。
形象地看, ϕ ∗ \phi_{*} ϕ ∗ M M M N N N ϕ ∗ X \phi_{*} X ϕ ∗ X ϕ ∗ X \phi_{*} X ϕ ∗ X N N N f f f f f f M M M X X X
向量场的拉回映射 向量场无法定义拉回映射。
假设存在拉回映射,设 ϕ : M → N \phi: M \to N ϕ : M → N ϕ ∗ : Γ ( T N ) → Γ ( T M ) \phi^*: \varGamma(TN) \to \varGamma (TM) ϕ ∗ : Γ ( T N ) → Γ ( T M ) N N N X X X M M M ϕ ∗ X \phi^* X ϕ ∗ X ϕ ∗ X \phi^* X ϕ ∗ X M M M f f f X X X N N N ϕ ∗ f \phi_* f ϕ ∗ f ( ϕ ∗ X ) ( f ) = X ( ϕ ∗ f ) (\phi^* X)(f) = X ( \phi_* f) ( ϕ ∗ X ) ( f ) = X ( ϕ ∗ f )
余切向量场的拉回映射 设 ϕ : M → N \phi: M \to N ϕ : M → N ω \omega ω N N N ϕ ∗ : Γ ( T ∗ N ) → Γ ( T ∗ M ) \phi^*:\varGamma(T^*N) \to \varGamma(T^*M) ϕ ∗ : Γ ( T ∗ N ) → Γ ( T ∗ M )
( ϕ ∗ ω ) ( X ) = ω ( ϕ ∗ X ) (\phi^* \omega) (X) = \omega (\phi_* X)
( ϕ ∗ ω ) ( X ) = ω ( ϕ ∗ X )
则 ϕ ∗ ω \phi^* \omega ϕ ∗ ω N N N ω \omega ω
由上给我们一些启发,即推前拉回映射维持张量结构 和张量之间相互作用 不变。张量结构不变指把 ( p , q ) (p,q) ( p , q ) ( p , q ) (p,q) ( p , q ) X X X ω \omega ω
ϕ ∗ f = f ∘ ϕ ϕ ∗ X = X ∘ ϕ ∗ ϕ ∗ ω = ω ∘ ϕ ∗ \phi^* f = f \circ \phi \qquad\phi_{*} X=X \circ \phi^{*} \qquad \phi^{*} \omega=\omega \circ \phi_{*}
ϕ ∗ f = f ∘ ϕ ϕ ∗ X = X ∘ ϕ ∗ ϕ ∗ ω = ω ∘ ϕ ∗
由此可以定义逆变张量的推前 和协变张量的拉回 。例如 T ∈ Γ ( ⊗ 0 , 2 T N ) T\in \varGamma\left(\otimes^{0,2} TN \right) T ∈ Γ ( ⊗ 0 , 2 T N ) N N N T T T ϕ ∗ T ∈ Γ ( ⊗ 0 , 2 T M ) \phi^* T \in \varGamma\left(\otimes^{0,2} TM \right) ϕ ∗ T ∈ Γ ( ⊗ 0 , 2 T M ) ( ϕ ∗ T ) ( X , Y ) = T ( ϕ ∗ X , ϕ ∗ Y ) , ∀ X , Y ∈ Γ ( T M ) \left(\phi^{*} T\right)(X, Y)=T\left(\phi_{*} X, \phi_{*} Y\right),\forall X, Y \in \varGamma(TM) ( ϕ ∗ T ) ( X , Y ) = T ( ϕ ∗ X , ϕ ∗ Y ) , ∀ X , Y ∈ Γ ( T M )
特殊地,若 ϕ \phi ϕ ϕ − 1 \phi^{-1} ϕ − 1
ϕ ∗ f = f ∘ ϕ − 1 ϕ ∗ X = X ∘ ϕ ∗ ϕ ∗ ω = ω ∘ ϕ ∗ \phi_* f = f \circ\phi^{-1} \qquad \phi^{*} X=X \circ \phi_{*} \qquad \phi_{*} \omega=\omega \circ \phi^{*}
ϕ ∗ f = f ∘ ϕ − 1 ϕ ∗ X = X ∘ ϕ ∗ ϕ ∗ ω = ω ∘ ϕ ∗
其中 f f f X X X ω \omega ω
/* 注:若 ϕ \phi ϕ ( ϕ − 1 ) ∗ = ϕ ∗ (\phi^{-1})^*= \phi_* ( ϕ − 1 ) ∗ = ϕ ∗ ( ϕ − 1 ) ∗ = ϕ ∗ (\phi^{-1})_*= \phi^* ( ϕ − 1 ) ∗ = ϕ ∗
张量场的拉回映射 设 ϕ : M → N \phi: M \to N ϕ : M → N 微分同胚 ,T ∈ Γ ( ⊗ p , q T N ) T \in \varGamma\left(\otimes^{p,q} TN \right) T ∈ Γ ( ⊗ p , q T N ) ϕ ∗ : Γ ( ⊗ p , q T N ) → Γ ( ⊗ p , q T M ) \phi^*: \varGamma\left(\otimes^{p,q} TN \right) \to \varGamma\left(\otimes^{p,q} TM \right) ϕ ∗ : Γ ( ⊗ p , q T N ) → Γ ( ⊗ p , q T M )
( ϕ ∗ T ) ( ω 1 , ⋯ , ω p , X 1 , ⋯ , X q ) = T ( ϕ ∗ ω 1 , ⋯ , ϕ ∗ ω p , ϕ ∗ X 1 , ⋯ , ϕ ∗ X q ) (\phi^* T) (\omega_1,\cdots,\omega_p,X_1,\cdots,X_q) = T(\phi_* \omega_1 ,\cdots,\phi_* \omega_p,\phi_* X_1,\cdots,\phi_* X_q)
( ϕ ∗ T ) ( ω 1 , ⋯ , ω p , X 1 , ⋯ , X q ) = T ( ϕ ∗ ω 1 , ⋯ , ϕ ∗ ω p , ϕ ∗ X 1 , ⋯ , ϕ ∗ X q )
设流形 M M M N N N { x μ } \{x^\mu\} { x μ } { x ′ μ } \{x^{\prime\mu}\} { x ′ μ }
( ϕ ∗ T ) μ 1 ⋯ μ p ν 1 ⋯ ν q = ( ϕ ∗ T ) ( d x μ 1 , ⋯ , d x μ p , ∂ ∂ x ν 1 , ⋯ , ∂ ∂ x ν q ) = T ( ϕ ∗ d x μ 1 , ⋯ , ϕ ∗ d x μ p , ϕ ∗ ∂ ∂ x ν 1 , ⋯ , ϕ ∗ ∂ ∂ x ν q ) \begin{aligned}
&\quad\,\,(\phi^* T)^{\mu_1\cdots \mu_p}{_{\nu_1\cdots\nu_q}} \\
&= (\phi^* T)\left(\mathrm{d} x^{\mu_1},\cdots,\mathrm{d} x^{\mu_p},\frac{\partial}{\partial x^{\nu_1}},\cdots,\frac{\partial}{\partial x^{\nu_q}}\right) \\
&= T \left(\phi_*\mathrm{d} x^{\mu_1},\cdots,\phi_*\mathrm{d} x^{\mu_p},\phi_*\frac{\partial}{\partial x^{\nu_1}},\cdots,\phi_*\frac{\partial}{\partial x^{\nu_q}}\right)
\end{aligned}
( ϕ ∗ T ) μ 1 ⋯ μ p ν 1 ⋯ ν q = ( ϕ ∗ T ) ( d x μ 1 , ⋯ , d x μ p , ∂ x ν 1 ∂ , ⋯ , ∂ x ν q ∂ ) = T ( ϕ ∗ d x μ 1 , ⋯ , ϕ ∗ d x μ p , ϕ ∗ ∂ x ν 1 ∂ , ⋯ , ϕ ∗ ∂ x ν q ∂ )
ϕ ∗ d x μ \phi_*\mathrm{d} x^{\mu} ϕ ∗ d x μ ϕ ∗ ∂ ∂ x μ \phi_*\frac{\partial}{\partial x^\mu} ϕ ∗ ∂ x μ ∂ ϕ \phi ϕ
张量场的推前映射 设 ϕ : M → N \phi: M \to N ϕ : M → N 微分同胚 ,T ∈ Γ ( ⊗ p , q T M ) T \in \varGamma\left(\otimes^{p,q} TM \right) T ∈ Γ ( ⊗ p , q T M ) ϕ ∗ : Γ ( ⊗ p , q T N ) → Γ ( ⊗ p , q T M ) \phi_*: \varGamma\left(\otimes^{p,q} TN \right) \to \varGamma\left(\otimes^{p,q} TM \right) ϕ ∗ : Γ ( ⊗ p , q T N ) → Γ ( ⊗ p , q T M )
( ϕ ∗ T ) ( ω 1 , ⋯ , ω p , X 1 , ⋯ , X q ) = T ( ϕ ∗ ω 1 , ⋯ , ϕ ∗ ω p , ϕ ∗ X 1 , ⋯ , ϕ ∗ X q ) (\phi_* T) (\omega_1,\cdots,\omega_p,X_1,\cdots,X_q) = T(\phi^* \omega_1 ,\cdots,\phi^* \omega_p,\phi^* X_1,\cdots,\phi^* X_q)
( ϕ ∗ T ) ( ω 1 , ⋯ , ω p , X 1 , ⋯ , X q ) = T ( ϕ ∗ ω 1 , ⋯ , ϕ ∗ ω p , ϕ ∗ X 1 , ⋯ , ϕ ∗ X q )
设流形 M M M N N N { x μ } \{x^\mu\} { x μ } { x ′ μ } \{x^{\prime\mu}\} { x ′ μ }
( ϕ ∗ T ) μ 1 ⋯ μ p ν 1 ⋯ ν q = ( ϕ ∗ T ) ( d x μ 1 , ⋯ , d x μ p , ∂ ∂ x ν 1 , ⋯ , ∂ ∂ x ν q ) = T ( ϕ ∗ d x μ 1 , ⋯ , ϕ ∗ d x μ p , ϕ ∗ ∂ ∂ x ν 1 , ⋯ , ϕ ∗ ∂ ∂ x ν q ) \begin{aligned}
&\quad\,\,(\phi_* T)^{\mu_1\cdots \mu_p}{_{\nu_1\cdots\nu_q}} \\
&= (\phi_* T)\left(\mathrm{d} x^{\mu_1},\cdots,\mathrm{d} x^{\mu_p},\frac{\partial}{\partial x^{\nu_1}},\cdots,\frac{\partial}{\partial x^{\nu_q}}\right) \\
&= T \left(\phi^*\mathrm{d} x^{\mu_1},\cdots,\phi^*\mathrm{d} x^{\mu_p},\phi^*\frac{\partial}{\partial x^{\nu_1}},\cdots,\phi^*\frac{\partial}{\partial x^{\nu_q}}\right)
\end{aligned}
( ϕ ∗ T ) μ 1 ⋯ μ p ν 1 ⋯ ν q = ( ϕ ∗ T ) ( d x μ 1 , ⋯ , d x μ p , ∂ x ν 1 ∂ , ⋯ , ∂ x ν q ∂ ) = T ( ϕ ∗ d x μ 1 , ⋯ , ϕ ∗ d x μ p , ϕ ∗ ∂ x ν 1 ∂ , ⋯ , ϕ ∗ ∂ x ν q ∂ )
ϕ ∗ d x μ \phi^*\mathrm{d} x^{\mu} ϕ ∗ d x μ ϕ ∗ ∂ ∂ x μ \phi^*\frac{\partial}{\partial x^\mu} ϕ ∗ ∂ x μ ∂ ϕ \phi ϕ
见电动力学讲义。
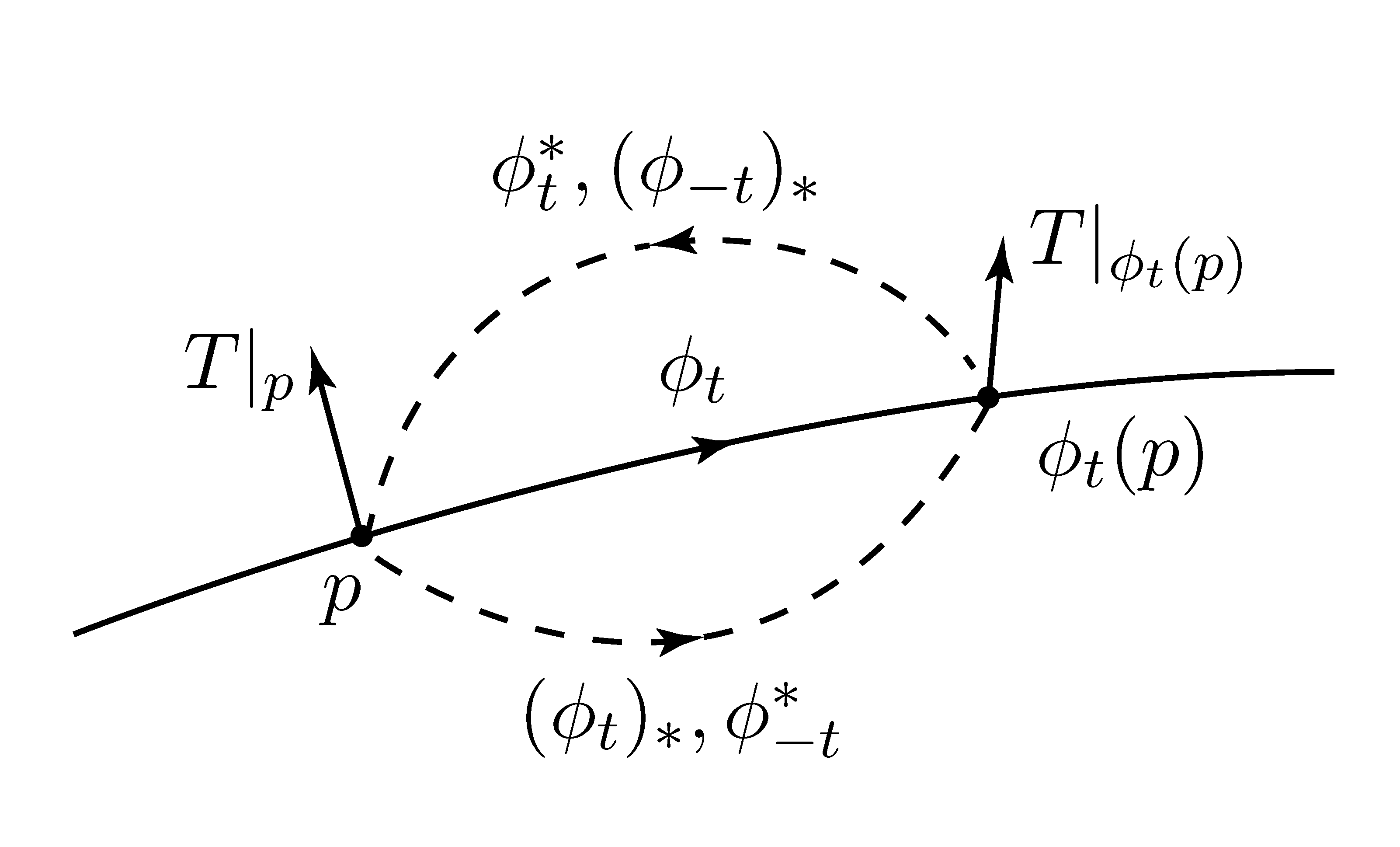
单参数变换群一节中讲过,给定向量场 X X X { ϕ t } ( t ∈ R ) \{\phi_t\} (t \in \mathbb{R}) { ϕ t } ( t ∈ R ) ϕ t \phi_t ϕ t X X X t t t p p p ϕ t ( p ) \phi_t(p) ϕ t ( p )
由于 ϕ t \phi_t ϕ t p p p t t t T T T X X X p p p t → 0 t \to 0 t → 0 t t t X X X
李导数 给定向量场 X X X T ∈ Γ ( ⊗ p , q T M ) T \in \varGamma\left(\otimes^{p,q} TM \right) T ∈ Γ ( ⊗ p , q T M ) L X T \mathcal{L}_X T L X T
L X T = lim t → 0 ϕ t ∗ ( T ∣ ϕ t ) − T t \mathcal{L}_X T = \lim_{t \to 0} \frac{\phi^*_t (T|_{\phi_t})-T}{t}
L X T = t → 0 lim t ϕ t ∗ ( T ∣ ϕ t ) − T
其中 ϕ t \phi_t ϕ t X X X T ∣ ϕ t T|_{\phi_t} T ∣ ϕ t ϕ t \phi_t ϕ t T ∣ ϕ t ( p ) T|_{\phi_t(p)} T ∣ ϕ t ( p ) p p p
( L X T ) ∣ p = lim t → 0 ϕ t ∗ ( T ∣ ϕ t ( p ) ) − T ∣ p t \left(\mathcal{L}_X T\right)|_p = \lim_{t \to 0} \frac{\phi^*_t (T|_{\phi_t(p)})-T|_p}{t}
( L X T ) ∣ p = t → 0 lim t ϕ t ∗ ( T ∣ ϕ t ( p ) ) − T ∣ p
李导数的定义不需要流形 M M M g g g ∇ \nabla ∇
双线性:L λ X + μ Y T = λ L X T + μ L Y T , L X ( λ T + μ S ) = λ L X T + μ L X S \mathcal{L}_{\lambda X+\mu Y} T = \lambda \mathcal{L}_{X} T + \mu \mathcal{L}_{Y} T,\ \mathcal{L}_X (\lambda T+\mu S)= \lambda \mathcal{L}_{X} T+ \mu\mathcal{L}_{X} S L λ X + μ Y T = λ L X T + μ L Y T , L X ( λ T + μ S ) = λ L X T + μ L X S λ , μ , ∈ R \lambda,\mu,\in \R λ , μ , ∈ R
第一分量Leibniz律:L f X Y = f L X Y − ( Y f ) X \mathcal{L}_{f X} Y = f \mathcal{L}_{X} Y - (Yf) X L f X Y = f L X Y − ( Y f ) X f ∈ C ∞ ( M ) f \in C^\infty(M) f ∈ C ∞ ( M )
第二分量Leibniz律:L X ( T ⊗ S ) = L X T ⊗ S + T ⊗ L X S \mathcal{L}_X \left(T\otimes S\right) = \mathcal{L}_X T\otimes S+T \otimes \mathcal{L}_X S L X ( T ⊗ S ) = L X T ⊗ S + T ⊗ L X S T , S T,S T , S
L X f = X f \mathcal{L}_X f = X f L X f = X f X X X f f f
L X Y = [ X , Y ] \mathcal{L}_X Y = [X,Y] L X Y = [ X , Y ] X , Y X,Y X , Y ⟹ L X Y = ∇ X Y − ∇ Y X \implies \mathcal{L}_X Y = \nabla_X Y -\nabla_Y X ⟹ L X Y = ∇ X Y − ∇ Y X ∇ \nabla ∇
Proof
根据李导数的定义,有
( L X Y ) ∣ p ( f ) = lim t → 0 ϕ t ∗ ( Y ∣ ϕ t ( p ) ) − Y ∣ p t ( f ) = lim t → 0 1 t [ Y ∣ ϕ t ( p ) ( ϕ t ∗ f ) − Y p f ] = lim t → 0 1 t [ Y ∣ ϕ t ( p ) ( f ∘ ϕ t − 1 ) − Y p f ] = lim t → 0 1 t [ Y ∣ ϕ t ( p ) ( f ∘ ϕ − t ) − Y p f ] ≈ lim t → 0 1 t [ Y ∣ ϕ t ( p ) ( f − t X f ) − Y p f ] = lim t → 0 1 t [ Y ∣ ϕ t ( p ) f − Y p f ] − Y ( X f ) = lim t → 0 1 t [ ( Y f ) ∣ ϕ t ( p ) − ( Y f ) ∣ p ] − Y p ( X f ) = X p ( Y f ) − Y p ( X f ) = [ X , Y ] p f \begin{aligned}
\left(\mathcal{L}_X Y\right)|_p (f) &= \lim_{t \to 0} \frac{\phi^*_t (Y|_{\phi_t(p)})-Y|_p}{t} (f) \\
&= \lim_{t \to 0} \frac{1}{t} \left[ Y|_{\phi_t(p)} (\phi_{t*}f) -Y_p f \right] \\
&= \lim_{t \to 0} \frac{1}{t} \left[ Y|_{\phi_t(p)} \left( f\circ \phi_t^{-1} \right) -Y_p f \right] \\
&= \lim_{t \to 0} \frac{1}{t} \left[ Y|_{\phi_t(p)} \left( f\circ \phi_{-t} \right) -Y_p f \right] \\
&\approx \lim_{t \to 0} \frac{1}{t} \left[ Y|_{\phi_t(p)} \left( f -tXf \right) -Y_p f \right] \\
&= \lim_{t \to 0} \frac{1}{t} \left[ Y|_{\phi_t(p)} f -Y_p f \right]- Y(Xf)\\
&= \lim_{t \to 0} \frac{1}{t} \left[ (Yf)|_{\phi_t(p)}-(Yf)|_p \right]- Y_p(Xf) \\
&= X_p (Yf)- Y_p(Xf) = [X,Y]_p f\\
\end{aligned}
( L X Y ) ∣ p ( f ) = t → 0 lim t ϕ t ∗ ( Y ∣ ϕ t ( p ) ) − Y ∣ p ( f ) = t → 0 lim t 1 [ Y ∣ ϕ t ( p ) ( ϕ t ∗ f ) − Y p f ] = t → 0 lim t 1 [ Y ∣ ϕ t ( p ) ( f ∘ ϕ t − 1 ) − Y p f ] = t → 0 lim t 1 [ Y ∣ ϕ t ( p ) ( f ∘ ϕ − t ) − Y p f ] ≈ t → 0 lim t 1 [ Y ∣ ϕ t ( p ) ( f − t X f ) − Y p f ] = t → 0 lim t 1 [ Y ∣ ϕ t ( p ) f − Y p f ] − Y ( X f ) = t → 0 lim t 1 [ ( Y f ) ∣ ϕ t ( p ) − ( Y f ) ∣ p ] − Y p ( X f ) = X p ( Y f ) − Y p ( X f ) = [ X , Y ] p f
其中关键之处在于第五步利用了 f ∘ ϕ t = f + t X f + ο ( t ) f\circ\phi_t = f+t Xf + \omicron(t) f ∘ ϕ t = f + t X f + ο ( t ) Y f Yf Y f L X f = X f = lim 1 t ( f ∣ ϕ t − f ) \mathcal{L}_X f = X f=\lim\frac{1}{t} \left( f|_{\phi_t}-f \right) L X f = X f = lim t 1 ( f ∣ ϕ t − f ) L X Y = [ X , Y ] \mathcal{L}_X Y = [X,Y] L X Y = [ X , Y ]
T ( X , Y ) = ∇ X Y − ∇ Y X − [ X , Y ] = 0 T(X,Y) = \nabla_X Y -\nabla_Y X-[X,Y]=0
T ( X , Y ) = ∇ X Y − ∇ Y X − [ X , Y ] = 0
就得到李导数用无挠联络表示的推论。
( L X ω ) ( Y ) = X [ ω ( Y ) ] − ω [ X , Y ] (\mathcal{L}_X \omega) (Y) = X\left[ \omega(Y)\right] - \omega[X,Y] ( L X ω ) ( Y ) = X [ ω ( Y ) ] − ω [ X , Y ] ω \omega ω
对于任意 ( p , q ) (p,q) ( p , q )
( L X T ) ( ω 1 , ⋯ , ω p , Y 1 , ⋯ , Y q ) = X [ T ( ω 1 , ⋯ , ω p , Y 1 , ⋯ , Y q ) ] + ∑ i = 1 p T ( ω 1 , ⋯ , L X ω i , ⋯ , ω p , Y 1 , ⋯ , Y q ) + ∑ i = 1 q T ( ω 1 , ⋯ , ω p , Y 1 , ⋯ , L X Y i , ⋯ , Y q ) \begin{aligned}
\left( \mathcal{L}_X T \right) \left(\omega_1,\cdots,\omega_p,Y_1,\cdots,Y_q \right) &= X \left[T \left(\omega_1,\cdots,\omega_p,Y_1,\cdots,Y_q \right)\right] + \sum_{i=1}^p T\left(\omega_1,\cdots,\mathcal{L}_X \omega_i,\cdots,\omega_p,Y_1,\cdots,Y_q \right) \\
&\quad\, + \sum_{i=1}^q T\left(\omega_1,\cdots,\omega_p,Y_1,\cdots,\mathcal{L}_X Y_i,\cdots,Y_q \right)
\end{aligned}
( L X T ) ( ω 1 , ⋯ , ω p , Y 1 , ⋯ , Y q ) = X [ T ( ω 1 , ⋯ , ω p , Y 1 , ⋯ , Y q ) ] + i = 1 ∑ p T ( ω 1 , ⋯ , L X ω i , ⋯ , ω p , Y 1 , ⋯ , Y q ) + i = 1 ∑ q T ( ω 1 , ⋯ , ω p , Y 1 , ⋯ , L X Y i , ⋯ , Y q )
Proof
与性质5的证明类似,但需要注意 T T T ω i → ω i + t L X ω i , Y i → Y i + t L X Y i \omega_i \to \omega_i + t \mathcal{L}_X \omega_i, Y_i \to Y_i + t \mathcal{L}_X Y_i ω i → ω i + t L X ω i , Y i → Y i + t L X Y i T ( ω + t L X ω ; Y + t L X Y ) T(\omega + t \mathcal{L}_X \omega \, ; Y+t \mathcal{L}_X Y) T ( ω + t L X ω ; Y + t L X Y ) ο ( t ) \omicron(t) ο ( t ) t 2 T ( L X ω i , L X Y i ) t^2 T(\mathcal{L}_X \omega_i, \mathcal{L}_X Y_i) t 2 T ( L X ω i , L X Y i )
[ L X , L Y ] = L [ X , Y ] \left[ \mathcal{L}_X, \mathcal{L}_Y\right] = \mathcal{L}_{[X,Y]} [ L X , L Y ] = L [ X , Y ]
李导数和协变导数各自规定了一种比较不同两点的张量的方法,均具有线性性和 Leibniz 律。
李导数定义来源于流形的光滑结构,是光滑流形自带的算符,不需要流形上的附加结构;协变导数可以在任何向量丛上定义,但需要额外的人工信息来定义,需要指定联络系数 Γ \Gamma Γ
李导数 ( L X T ) ∣ p \left(\mathcal{L}_X T\right)|_p ( L X T ) ∣ p X X X p p p ( ∇ X T ) ∣ p (\nabla_X T)|_p ( ∇ X T ) ∣ p X X X p p p X p X_p X p
适配坐标系 若向量场 X X X ∂ ∂ x 1 \frac{\partial}{\partial x^1} ∂ x 1 ∂ X X X
适配坐标系中,沿 X X X L X \mathcal{L}_X L X ∂ ∂ x 1 \frac{\partial}{\partial x^1} ∂ x 1 ∂
等度规映射 若微分同胚 ϕ : M → M \phi:M \to M ϕ : M → M ϕ ∗ g = g \phi^* g =g ϕ ∗ g = g ϕ \phi ϕ
Killing向量场 设 X X X ( M , g ) (M, g) ( M , g ) X X X ϕ t \phi_t ϕ t X X X ( M , g ) (M, g) ( M , g )
Killing方程 成为 Killing 向量场的充分必要条件是满足 Killing 方程。由 Killing 向量场的定义知,若 X X X
L X g = 0 \mathcal{L}_X g =0
L X g = 0
或者写作
X g ( Y , Z ) = g ( [ X , Y ] , Z ) + g ( Y , [ X , Z ] ) ∀ X , Y , Z ∈ Γ ( T M ) X g(Y,Z) =g([X,Y],Z) + g(Y,[X,Z]) \qquad \forall X, Y,Z\in \Gamma(T M)
X g ( Y , Z ) = g ( [ X , Y ] , Z ) + g ( Y , [ X , Z ] ) ∀ X , Y , Z ∈ Γ ( T M )
若 ∇ \nabla ∇
g ( ∇ Y X , Z ) + g ( Y , ∇ Z X ) = 0 ∀ Y , Z ∈ Γ ( T M ) g\left(\nabla_{Y} X, Z\right)+ g\left( Y, \nabla_{Z} X\right)=0 \qquad \forall Y, Z \in \Gamma(T M)
g ( ∇ Y X , Z ) + g ( Y , ∇ Z X ) = 0 ∀ Y , Z ∈ Γ ( T M )
其分量形式为
∇ μ X ν + ∇ ν X μ = 0 \nabla_\mu X_\nu + \nabla_\nu X_\mu = 0
∇ μ X ν + ∇ ν X μ = 0
定理:黎曼流形 ( M , g ) (M, g) ( M , g ) n ( n + 1 ) / 2 n(n+1)/2 n ( n + 1 ) / 2 n = dim M n = \dim M n = dim M
Killing 方程 L X g = 0 \mathcal{L}_X g =0 L X g = 0