本篇文章是西安交大《计算物理与程序设计》课程的笔记,程序语言为 MATLAB。内容主要包括用打靶法求解定态Schrodinger方程的能级,以及用Thomas算法求解化为三对角线性系统的含时薛定谔方程。
一维定态Schrodinger方程为
H φ = E φ H \varphi = E \varphi
H φ = E φ
− ℏ 2 2 m d 2 φ d x 2 + V φ = E φ -\frac{\hbar^2}{2m} \frac{\mathrm{d}^{2}\varphi}{\mathrm{d}x^2} + V\varphi=E\varphi
− 2 m ℏ 2 d x 2 d 2 φ + V φ = E φ
这实质上是二阶常微分方程的本征值问题,其中 E E E 0 0 0 ± a \pm a ± a
φ ( ± a ) = 0 \varphi(\pm a)=0
φ ( ± a ) = 0
这样一来便可以使用打靶法配合 Numerov 算法求解此边值问题。此处初值为 φ ( − a ) = 0 \varphi(- a)=0 φ ( − a ) = 0 φ ′ ( − a ) = K \varphi^\prime (-a) = K φ ′ ( − a ) = K K K K φ ( a ) = 0 \varphi(a)=0 φ ( a ) = 0 E E E
/* 注:子弹不是 φ ′ ( − a ) \varphi^\prime (-a) φ ′ ( − a ) E E E φ ′ ( − a ) \varphi^\prime (-a) φ ′ ( − a )
处理斜势阱壁需要使用双向积分方法 ,以保证经典禁戒区的波函数不包含指数增长成分。
如图所示,选取能级与势阱的交点为接合点 x c x_c x c
1 R [ φ < ′ ( x c − ) − φ > ′ ( x c + ) ] = 0 \frac{1}{R}\left[ \varphi_<^\prime (x_c^-) -\varphi_>^\prime (x_c^+) \right] = 0
R 1 [ φ < ′ ( x c − ) − φ > ′ ( x c + ) ] = 0
其中 R R R x c x_c x c 二分法误差限 δ \delta δ R R R 1 1 1
一维含时 Schrodinger 方程为
i ℏ ∂ ψ ∂ t = − ℏ 2 2 m ∂ 2 ψ ∂ x 2 + V ψ \mathrm{i} \hbar\frac{\partial \psi}{\partial t} = -\frac{\hbar^2}{2m} \frac{\partial^{2}{\psi}}{\partial{x}^{2}} + V\psi
i ℏ ∂ t ∂ ψ = − 2 m ℏ 2 ∂ x 2 ∂ 2 ψ + V ψ
按照 Crank-Nicolson 算法,等式右边的每个 ψ \psi ψ 1 2 ( ψ j + ψ j + 1 ) \frac{1}{2}\left(\psi^j + \psi^{j+1}\right) 2 1 ( ψ j + ψ j + 1 )
i ℏ ψ i j + 1 − ψ i j Δ t = − ℏ 2 2 m 1 2 [ ψ i + 1 j − 2 ψ i j + ψ i − 1 j ( Δ x ) 2 + ψ i + 1 j + 1 − 2 ψ i j + 1 + ψ i − 1 j + 1 ( Δ x ) 2 ] + 1 2 V i ( ψ i j + ψ i j + 1 ) \mathrm{i} \hbar\frac{\psi^{j+1}_i-\psi^{j}_i}{\Delta t} = -\frac{\hbar^2}{2m} \frac{1}{2} \left[\frac{\psi_{i+1}^j-2\psi_i^j+\psi_{i-1}^j}{(\Delta x)^2} + \frac{\psi_{i+1}^{j+1}-2\psi_i^{j+1}+\psi_{i-1}^{j+1}}{(\Delta x)^2} \right] + \frac{1}{2} V_i\left(\psi^j_i + \psi^{j+1}_i\right)
i ℏ Δ t ψ i j + 1 − ψ i j = − 2 m ℏ 2 2 1 [ ( Δ x ) 2 ψ i + 1 j − 2 ψ i j + ψ i − 1 j + ( Δ x ) 2 ψ i + 1 j + 1 − 2 ψ i j + 1 + ψ i − 1 j + 1 ] + 2 1 V i ( ψ i j + ψ i j + 1 )
定义 r = i ℏ Δ t 2 m ( Δ x ) 2 r=\frac{\mathrm{i} \hbar \Delta t }{2m(\Delta x)^2} r = 2 m ( Δ x ) 2 i ℏ Δ t
− r 2 ψ i − 1 j + 1 + ( 1 + r + i Δ t 2 ℏ V i ) ψ i j + 1 − r 2 ψ i + 1 j + 1 = r 2 ψ i + 1 j + ( 1 − r − i Δ t 2 ℏ V i ) ψ i j + r 2 ψ i − 1 j -\frac{r}{2} \psi_{i-1}^{j+1}+\left(1+r+\frac{\mathrm{i} \Delta t}{2 \hbar}V_i\right) \psi_{i}^{j+1} - \frac{r}{2}\psi_{i+1}^{j+1} = \frac{r}{2} \psi_{i+1}^{j}+\left(1-r-\frac{\mathrm{i} \Delta t}{2 \hbar}V_i\right)\psi_{i}^{j} + \frac{r}{2}\psi_{i-1}^{j}
− 2 r ψ i − 1 j + 1 + ( 1 + r + 2 ℏ i Δ t V i ) ψ i j + 1 − 2 r ψ i + 1 j + 1 = 2 r ψ i + 1 j + ( 1 − r − 2 ℏ i Δ t V i ) ψ i j + 2 r ψ i − 1 j
仍然为三对角方程,使用附录中Thomas算法 即可求解。
差分方程亦可通过算符的形式写出。定义哈密顿量算符
H = − ℏ 2 2 m δ 2 + V H = -\frac{\hbar^2}{2m} \delta^2 +V
H = − 2 m ℏ 2 δ 2 + V
系统的演化可以写为
∣ ψ ( t + Δ t ) ⟩ = e − i H Δ t / ℏ ∣ ψ ( t ) ⟩ = e − i H Δ t / 2 ℏ e i H Δ t / 2 ℏ ∣ ψ ( t ) ⟩ ⟹ e i H Δ t / 2 ℏ ∣ ψ ( t + Δ t ) ⟩ = e − i H Δ t / 2 ℏ ∣ ψ ( t ) ⟩ ⟹ ( 1 + i Δ t 2 ℏ H ) ψ ( t + Δ t ) = ( 1 − i Δ t 2 ℏ H ) ψ ( t ) \begin{aligned}
&|\psi(t+\Delta t)\rangle = \mathrm{e}^{-\mathrm{i}H\Delta t / \hbar}|\psi(t)\rangle=\frac{\mathrm{e}^{-\mathrm{i}H\Delta t/2\hbar}}{\mathrm{e}^{\mathrm{i}H\Delta t/2\hbar}} |\psi(t)\rangle \\
\implies \, & \mathrm{e}^{\mathrm{i}H\Delta t/2\hbar} |\psi(t+\Delta t)\rangle = \mathrm{e}^{-\mathrm{i}H\Delta t/2\hbar} |\psi(t)\rangle \\
\implies \, & \left( 1+ \frac{\mathrm{i}\Delta t}{2\hbar}H\right) \psi(t+\Delta t) = \left( 1- \frac{\mathrm{i}\Delta t}{2\hbar}H\right) \psi(t)
\end{aligned}
⟹ ⟹ ∣ ψ ( t + Δ t ) ⟩ = e − i H Δ t / ℏ ∣ ψ ( t ) ⟩ = e i H Δ t / 2 ℏ e − i H Δ t / 2 ℏ ∣ ψ ( t ) ⟩ e i H Δ t / 2 ℏ ∣ ψ ( t + Δ t ) ⟩ = e − i H Δ t / 2 ℏ ∣ ψ ( t ) ⟩ ( 1 + 2 ℏ i Δ t H ) ψ ( t + Δ t ) = ( 1 − 2 ℏ i Δ t H ) ψ ( t )
可以验证,结果与上述差分方程完全相同。实际计算中仍然需要使用差分方程。但算符形式好处在于可以推广到哈密顿量 H H H Computer Physics Communications 的文献。
实际计算中,可以进行一个小变换,令 χ i j = ψ i j + 1 + ψ i j \chi_i^j = \psi_{i}^{j+1} + \psi_{i}^{j} χ i j = ψ i j + 1 + ψ i j
− r 2 χ i − 1 j + ( 1 + r + i Δ t 2 ℏ V i ) χ i j − r 2 χ i + 1 j = 2 ψ i j -\frac{r}{2} \chi_{i-1}^j+\left(1+r+\frac{\mathrm{i} \Delta t}{2 \hbar}V_i\right) \chi_{i}^j - \frac{r}{2}\chi_{i+1}^j = 2\psi_{i}^{j}
− 2 r χ i − 1 j + ( 1 + r + 2 ℏ i Δ t V i ) χ i j − 2 r χ i + 1 j = 2 ψ i j
然后便可求解此三对角方程,注意在等式右边首项和末项加上 r 2 χ 1 j \frac{r}{2} \chi_1^j 2 r χ 1 j r 2 χ N j \frac{r}{2} \chi^j_N 2 r χ N j χ i j \chi_i^j χ i j ψ i j \psi_{i}^{j} ψ i j ψ i j + 1 \psi_i^{j+1} ψ i j + 1
在线性代数中,三对角矩阵是矩阵的一种。一个三对角矩阵的非零系数在如下的三条对角线上:主对角线、低对角线、高对角线。在许多物理问题中,三对角矩阵常常作为原始数据出现,因此它们本身是很重要的,这种矩阵仅有 2 n − 1 2n-1 2 n − 1
设主对角线上的元素为 n n n b \boldsymbol{b} b n − 1 n-1 n − 1 a \boldsymbol{a} a c \boldsymbol{c} c diag 命令生成
1 A = diag (b,0 ) + diag (a,-1 ) + diag (c,1 );
特殊地,若对角线上各个元素均相同,则可以用 ones 生成
1 A = diag (b*ones (n,1 ),0 ) + diag (a*ones (n-1 ,1 ),-1 ) + diag (c*ones (n-1 ,1 ),1 );
三对角线性方程组指形如
a i x i − 1 + b i x i + c i x i + 1 = d i a_{i}x_{i-1}+b_{i}x_{i}+c_{i}x_{i+1}=d_{i}
a i x i − 1 + b i x i + c i x i + 1 = d i
其中 a 1 = 0 a_1=0 a 1 = 0 c n = 0 c_n=0 c n = 0 A A A
A x = d A \boldsymbol{x} = \boldsymbol{d}
A x = d
[ b 1 c 1 a 1 b 2 c 2 a 2 ⋱ ⋱ ⋱ ⋱ c n − 2 a n − 2 b n − 1 c n − 1 a n − 1 b n ] [ x 1 x 2 x 3 ⋮ x n − 1 x n ] = [ d 1 d 2 d 3 ⋮ d n − 1 d n ] \begin{bmatrix}
b_1 & c_1 & & & & \\
a_1 & b_2 & c_2 & & & \\
& a_2 & \ddots & \ddots & & \\
& & \ddots & \ddots & c_{n-2} & \\
& & & a_{n-2} & b_{n-1} & c_{n-1} \\
& & & & a_{n-1} & b_n
\end{bmatrix}
\begin{bmatrix}
x_1 \\ x_2 \\ x_3 \\ \vdots \\ x_{n-1} \\ x_n
\end{bmatrix}=
\begin{bmatrix}
d_1 \\ d_2 \\ d_3 \\ \vdots \\ d_{n-1} \\ d_n
\end{bmatrix}
⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ b 1 a 1 c 1 b 2 a 2 c 2 ⋱ ⋱ ⋱ ⋱ a n − 2 c n − 2 b n − 1 a n − 1 c n − 1 b n ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ x 1 x 2 x 3 ⋮ x n − 1 x n ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ d 1 d 2 d 3 ⋮ d n − 1 d n ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤
对于三对角线性方程组,不必使用时间复杂度为 O ( n 3 ) O(n^3) O ( n 3 ) Thomas算法 达到仅 O ( n ) O(n) O ( n )
Thomas算法的MATLAB代码为
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 function x = tridiag (A,d) n = length (d); x = zeros (n,1 ); for i = 2 :n w = A(i ,i -1 )/A(i -1 ,i -1 ); A(i ,i ) = A(i ,i )-w*A(i -1 ,i ); d(i ) = d(i )-w*d(i -1 ); end x(n) = d(n)/A(n,n); for i = (n-1 ):(-1 ):1 x(i ) = (d(i )-A(i ,i +1 )*x(i +1 ))/A(i ,i ); end end
待更
求解Schrodinger方程过程中常常需要对波函数进行归一化,而波函数往往是离散点列而非连续函数,不方便调用 integral 进行积分。
这里提供一个 numint(X,Y) 函数,根据 X X X Y Y Y X X X trapz(X,Y) 。
1 2 3 4 5 6 7 8 9 10 11 12 function integration = numint (X,Y) N = length (X); if mod (N,2 ) == 0 integration = trapz(X,Y); else dx = X(2 ) - X(1 ); integration = dx/3 *(Y(1 )+Y(N)+4 *sum(Y(2 :2 :N))+2 *sum(Y(3 :2 :N-1 ))); end end
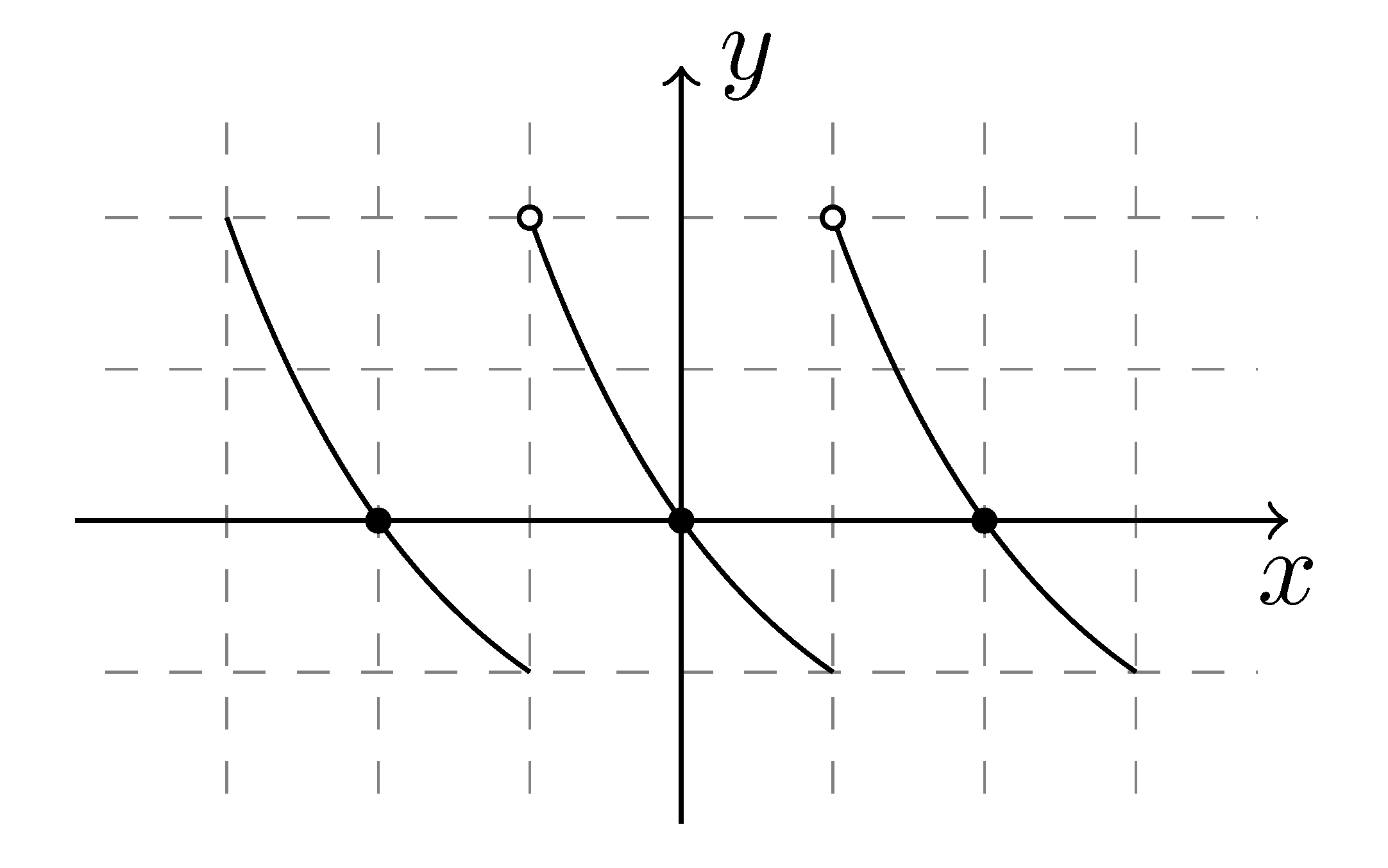
面对间断函数时,即便是预搜索二分法也难以找到函数零点。
如图所示,实心点为周期间断函数真正的零点,而空心点为间断点。预搜索二分法固然能判断并找到实心点作为零点,但在空心点两侧函数异号,预搜索认为此处也存在一个零点。无论二分区间 ( a , b ) (a,b) ( a , b ) ∣ a − b ∣ |a-b| ∣ a − b ∣ ε \varepsilon ε
处理方法是,引入二分法偏差返回值 deviation 和误差限 δ \delta δ deviation 定义为 ∣ a − b ∣ |a-b| ∣ a − b ∣ ε \varepsilon ε ∣ f ( a ) − f ( b ) ∣ |f(a)-f(b)| ∣ f ( a ) − f ( b ) ∣ deviation 应当甚小,能够小于给定的误差限 δ \delta δ ( a , b ) (a,b) ( a , b ) ∣ f ( a ) − f ( b ) ∣ |f(a)-f(b)| ∣ f ( a ) − f ( b ) ∣
因而可将二分法搜寻完成后的 deviation 是否小于 δ \delta δ deviation 大于 δ \delta δ root+step 开始重新搜索。以下为优化后的预搜索二分查找零点函数 prebisection(f,x0,step,epsilon,delta) 。
1 2 3 4 5 6 7 8 9 10 11 12 function root = prebisection (f,x0,step,epsilon,delta) while f(x0+step)*f(x0)>0 x0 = x0 + step; end [root,deviation] = bisection(f,x0,x0+step,epsilon); if deviation > delta root = prebisection(f,root+step,step,epsilon,delta); end end
二分查找零点参见计算物理第一篇文章中的 bisection.m 。