本文梳理一下光栅与光谱,插图主要来自钟锡华老师和赵凯华老师合编的《光学》。
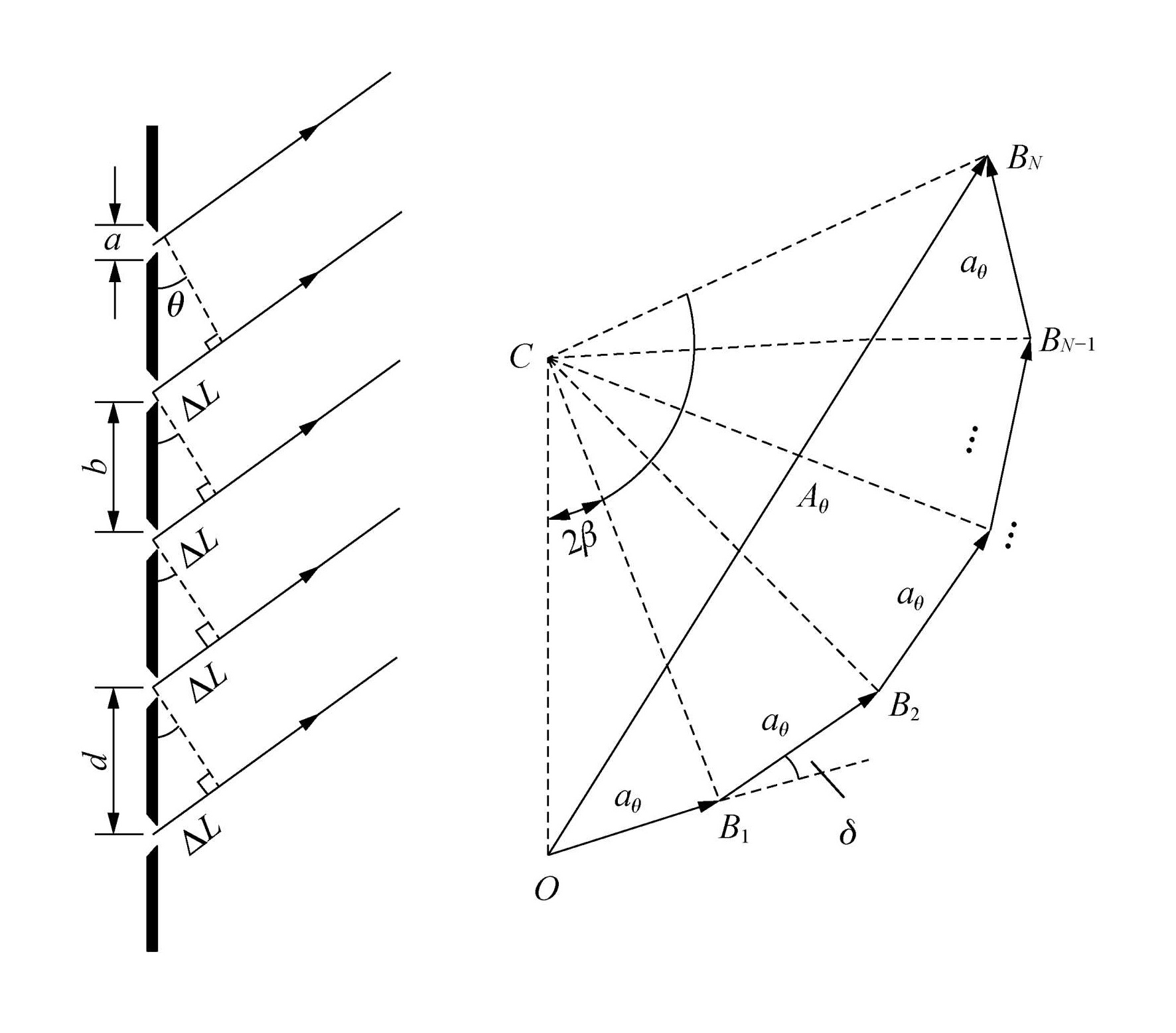
具有周期性的空间结构或光学性能的衍射屏,统称光栅。例如在一块不透明的障板上刻画出一系列等宽又等间隔的平行狭缝,就是一种简单的一维多缝光栅。在一张透明胶片上因曝光而记录的一组等宽又等间隔的平行干涉条纹,便是一块一维的正弦光栅。晶体由于内部原子排列具有空间周期性而成为天然的三维光栅。
下面讨论简单的 N N N
作符号约定如下
符号
说明
a a a 单个缝宽
b b b 缝间不透明部分的宽度
d d d 缝间距离,称为光栅常数
A 0 A_0 A 0 单缝衍射的振幅
通过矢量图易推得光栅衍射公式
I θ = A 0 2 ( sin α α ) 2 ( sin N β sin β ) 2 I_{\theta}=A_{0}^{2}\left(\frac{\sin \alpha}{\alpha}\right)^{2}\left(\frac{\sin N \beta}{\sin \beta}\right)^{2}
I θ = A 0 2 ( α sin α ) 2 ( sin β sin N β ) 2
其中
α = π a λ sin θ β = π d λ sin θ \alpha=\frac{\pi a}{\lambda} \sin \theta \qquad \beta=\frac{\pi d}{\lambda} \sin \theta
α = λ π a sin θ β = λ π d sin θ
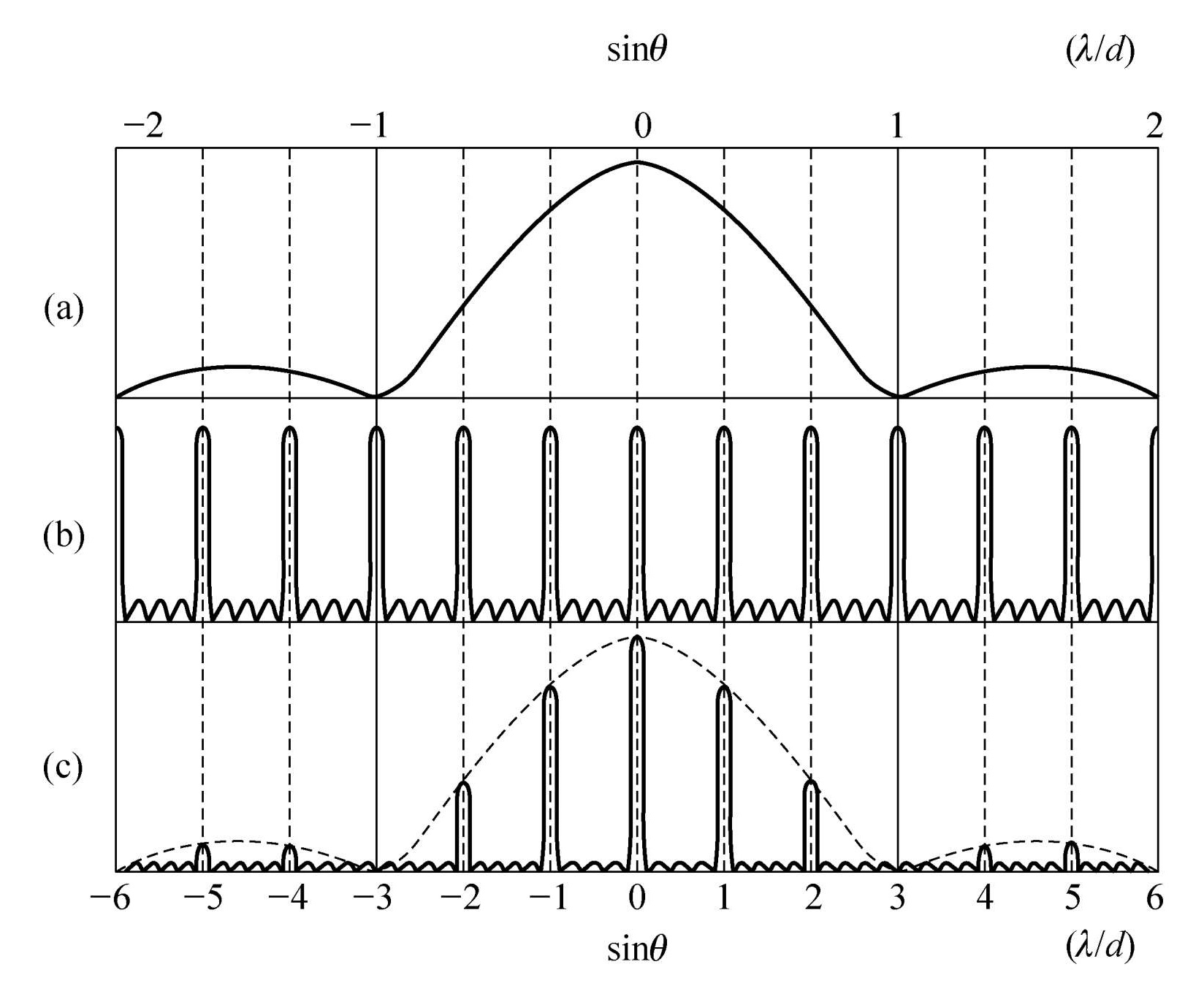
光栅衍射公式中的 ( sin α α ) 2 \left(\dfrac{\sin \alpha}{\alpha}\right)^{2} ( α sin α ) 2 ( sin N β sin β ) 2 \left(\dfrac{\sin N \beta}{\sin \beta}\right)^{2} ( sin β sin N β ) 2
若寻找各个极大的位置,只需令缝间干涉因子中 sin β = 0 \sin \beta =0 sin β = 0 sin N β = 0 \sin N \beta = 0 sin N β = 0 N 2 N^2 N 2
若寻找各个极小的位置,只需令 sin N β = 0 \sin N \beta = 0 sin N β = 0 sin β ≠ 0 \sin \beta \neq 0 sin β = 0 N − 1 N-1 N − 1
I max : sin β = 0 ⟹ d sin θ = k λ ( k ∈ N ) I_{\text{max}}:\sin \beta =0 \Longrightarrow d\sin \theta = k\lambda \ (k\in \mathbb{N})
I max : sin β = 0 ⟹ d sin θ = k λ ( k ∈ N )
I min : { sin N β = 0 sin β ≠ 0 ⟹ d sin θ = k ′ λ N ( k ′ ≠ N , 2 N , ⋯ ) I_{\text{min}}:\begin{cases} \sin N \beta = 0 \\ \sin \beta \neq 0 \end{cases} \Longrightarrow d \sin \theta = k^\prime \frac{\lambda}{N} \ (k^\prime \neq N,2N,\cdots)
I min : { sin N β = 0 sin β = 0 ⟹ d sin θ = k ′ N λ ( k ′ = N , 2 N , ⋯ )
两个主极大之间还存在一些次极大,由下式确定
I secmax : d d β ( sin N β sin β ) = 0 I_{\text{secmax}} : \frac{\mathrm{d}}{\mathrm{d}\beta}\left(\dfrac{\sin N \beta}{\sin \beta}\right) =0
I secmax : d β d ( sin β sin N β ) = 0
但次极大的数目可以直接从Lagrange中值定理中看出。每个极小之间必然存在一个极大,因为极小时的光强都是 0 0 0 N − 2 N-2 N − 2
由于单缝衍射因子的存在,并不是所有极大都能有效地发挥出来。倘若 sin β = 0 \sin \beta =0 sin β = 0 sin α = 0 \sin \alpha=0 sin α = 0 0 0 0
{ sin β = 0 sin α = 0 ⟹ { d sin θ = k λ a sin θ = l λ ⟹ k = d a l ( l ∈ N ) \begin{cases} \sin \beta = 0 \\ \sin \alpha = 0 \end {cases} \Longrightarrow \begin{cases} d\sin \theta = k\lambda \\ a\sin \theta = l \lambda \end{cases} \Longrightarrow k =\frac{d}{a} l \ (l \in \mathbb{N})
{ sin β = 0 sin α = 0 ⟹ { d sin θ = k λ a sin θ = l λ ⟹ k = a d l ( l ∈ N )
可见第 ± d a , ± 2 d a , ⋯ \pm \frac{d}{a}, \pm 2\frac{d}{a}, \cdots ± a d , ± 2 a d , ⋯ d d d a a a
主极大的位置:d sin θ = k λ d\sin \theta = k\lambda d sin θ = k λ
主极大的个数:∣ sin θ ∣ = ∣ k ∣ λ d ≤ 1 ⟹ ∣ k ∣ ≤ d λ |\sin \theta| = |k|\dfrac{\lambda}{d} \le 1 \Longrightarrow |k| \le \dfrac{d}{\lambda} ∣ sin θ ∣ = ∣ k ∣ d λ ≤ 1 ⟹ ∣ k ∣ ≤ λ d
主极大的半角宽度:Δ θ k = λ N d cos θ k \Delta \theta_k =\dfrac{\lambda}{N d \cos \theta_{k}} Δ θ k = N d cos θ k λ
/* 主极大的半角宽度见下面的正式推导 */
光谱是复色光经过分光系统分光后,被色散开的单色光按波长大小而依次排列的图案。
以光栅为例,一束混杂着 λ 1 = 589.0 n m , λ 2 = 589.6 n m \lambda_1 = 589.0 \mathrm{nm}, \lambda_2 =589.6\mathrm{nm} λ 1 = 5 8 9 . 0 n m , λ 2 = 5 8 9 . 6 n m k k k k k k 角距离 记为 δ θ k \delta \theta_k δ θ k k k k 线距离 记为 δ l k \delta l_k δ l k δ λ \delta \lambda δ λ 角色散本领 和线色散本领 ,记作 D θ D_\theta D θ D l D_l D l
D θ = δ θ δ λ D l = δ l δ λ D_\theta = \frac{\delta \theta}{\delta \lambda} \qquad D_l = \frac{\delta l}{\delta \lambda}
D θ = δ λ δ θ D l = δ λ δ l
其中下标 k k k k k k k k k
一般地,偏向角 δ \delta δ λ \lambda λ
但可以证明,沿产生最小偏向角的方向入射时,光谱线弯曲得最少。所以在光谱仪中棱镜通常是装在接近于产生最小偏向角的位置。因此棱镜的角色散本领 D θ D_\theta D θ
D θ = d δ m d λ D_\theta = \frac{\mathrm{d} \delta_{\mathrm{m}}}{\mathrm{d} \lambda}
D θ = d λ d δ m
我们已经知道了不同折射率棱镜的最小偏向角
n = sin α + δ m 2 sin α 2 n=\frac{\sin \frac{\alpha+\delta_m}{2}}{\sin \frac{\alpha}{2}}
n = sin 2 α sin 2 α + δ m
而不同波长的光在棱镜中的折射率不同,可用链式法则计算 D θ D_\theta D θ
D θ = d δ m d λ = d δ m d n d n d λ = ( d n d δ m ) − 1 d n d λ = 2 sin ( α / 2 ) 1 − n 2 sin 2 ( α / 2 ) ⋅ d n d λ D_{\theta}=\frac{\mathrm{d} \delta_{\mathrm{m}}}{\mathrm{d} \lambda}=\frac{\mathrm{d} \delta_{\mathrm{m}}}{\mathrm{d} n} \frac{\mathrm{d} n}{\mathrm{d} \lambda}=\left(\frac{\mathrm{d} n}{\mathrm{d} \delta_{\mathrm{m}}}\right)^{-1} \frac{\mathrm{d} n}{\mathrm{d} \lambda} = \frac{2 \sin (\alpha / 2)}{\sqrt{1-n^{2} \sin ^{2}(\alpha / 2)}} \cdot \frac{\mathrm{d} n}{\mathrm{d} \lambda}
D θ = d λ d δ m = d n d δ m d λ d n = ( d δ m d n ) − 1 d λ d n = 1 − n 2 sin 2 ( α / 2 ) 2 sin ( α / 2 ) ⋅ d λ d n
它又可以写为
D θ = b a d n d λ D_{\theta}=\frac{b}{a}\frac{\mathrm{d} n}{\mathrm{d} \lambda}
D θ = a b d λ d n
式中 b b b a a a
光栅的角色散本领看的是第 k k k
对光栅方程两边取微分,得到 d cos θ k δ θ = k δ λ d \cos \theta_{k} \delta \theta=k \delta \lambda d cos θ k δ θ = k δ λ
D θ = k d cos θ k D_{\theta}=\frac{k}{d \cos \theta_{k}}
D θ = d cos θ k k
得到结论:光栅的角色散本领与光栅常数 d d d k k k
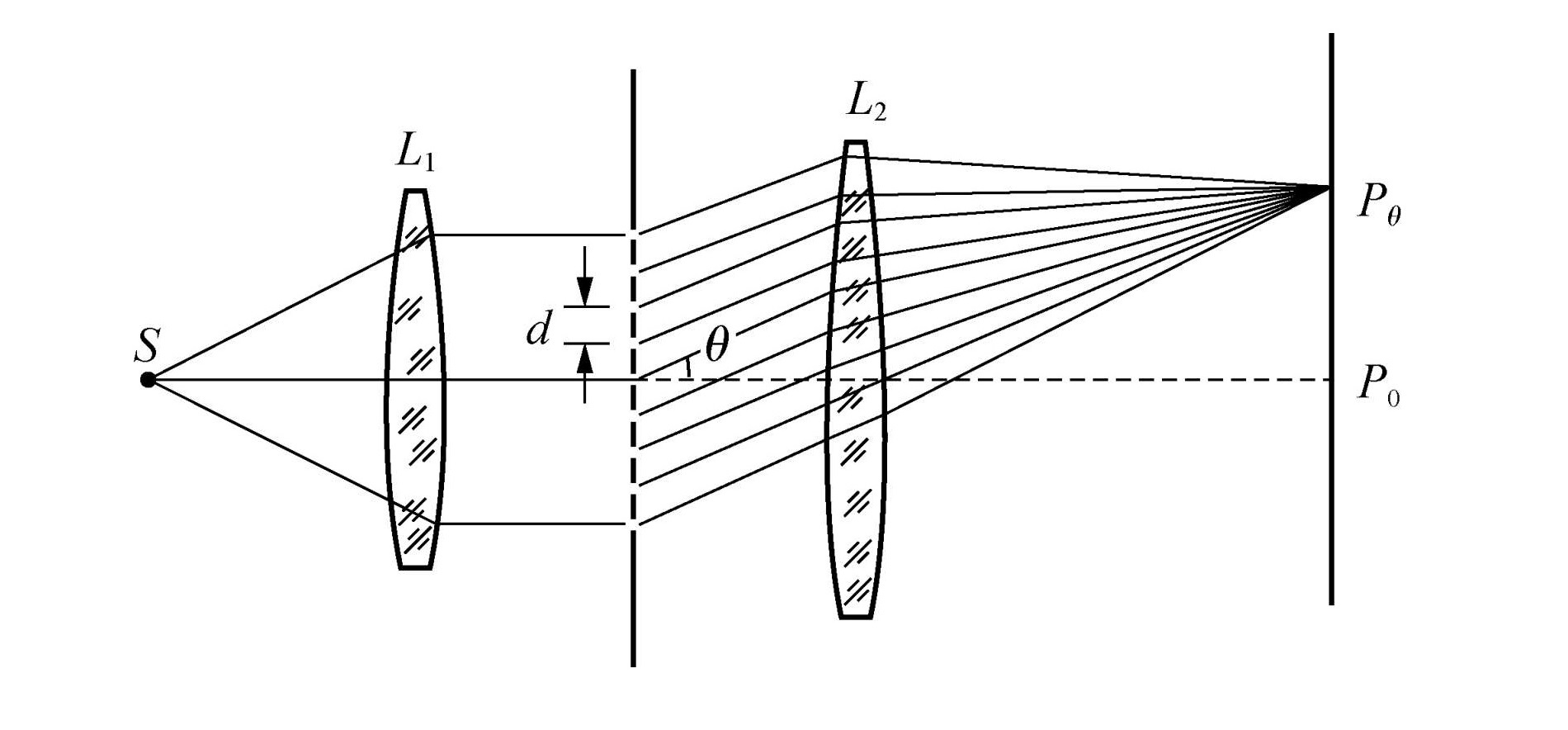
光栅的线色散本领需要结合具体装置,如图所示。
对于上述装置,设光栅后面聚焦物镜的焦距为 f f f δ l = f δ θ \delta l = f \delta \theta δ l = f δ θ
D l = f D θ = k f d cos θ k D_l = f D_\theta = \frac{kf}{d \cos \theta_{k}}
D l = f D θ = d cos θ k k f
得到结论:光栅的线色散本领还与焦矩 f f f N N N
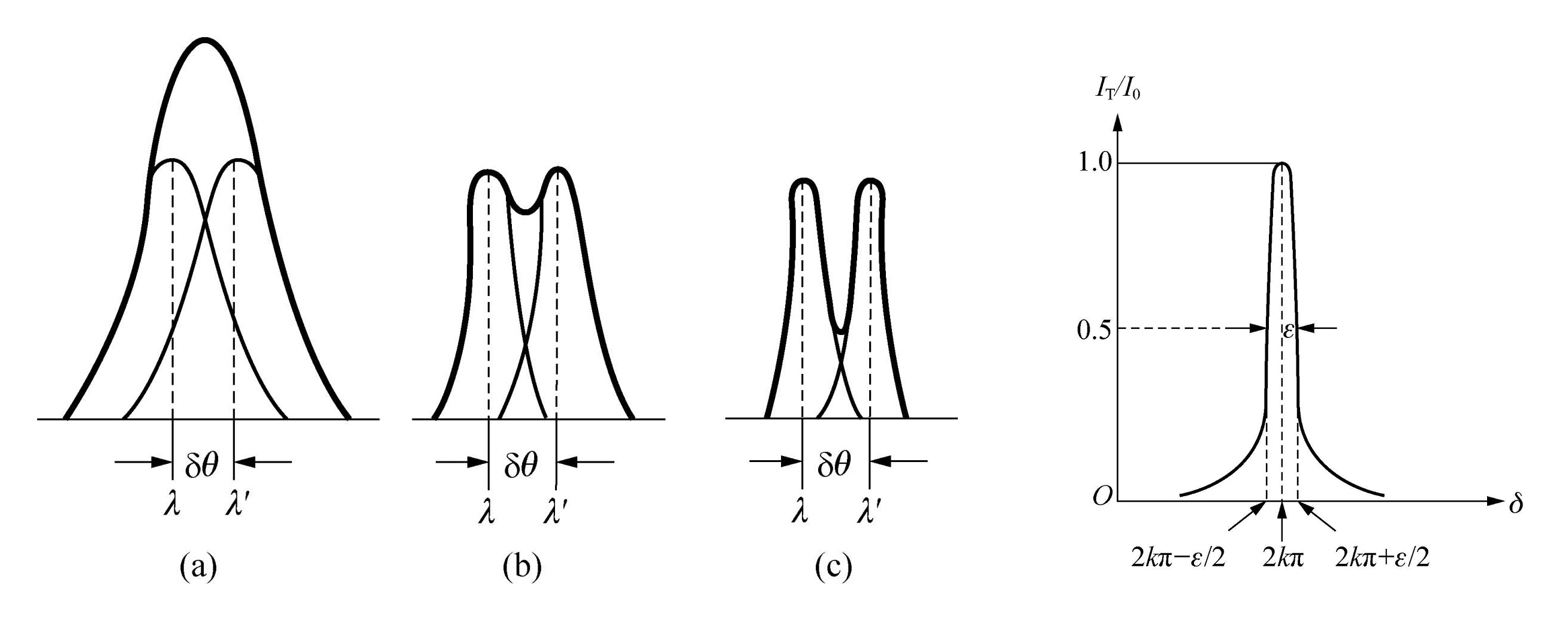
色散本领只反映谱线中心分离的程度,它不能说明两条谱线是否重叠。所以只有色散本领大还是不够的,要分辨波长很接近的谱线,仍需每条谱线都很细。设分光仪器能够分辨的最小波长差为 δ λ \delta \lambda δ λ
R = λ δ λ R = \frac{\lambda}{\delta \lambda}
R = δ λ λ
色分辨本领越大,分光仪器能够分辨的最小波长差越小,代表着分光仪器越精细。问题是,我们如何界定「能够分辨」?回忆瑞利判据:当两个像之间的角距离等于艾里斑的角半径时恰好能分清。我们作类似规定:当两条谱线之间的角距离 δ θ \delta \theta δ θ Δ θ \Delta \theta Δ θ
由判据 δ θ = Δ θ \delta \theta = \Delta \theta δ θ = Δ θ δ θ = D θ δ λ \delta \theta = D_\theta \delta \lambda δ θ = D θ δ λ Δ θ \Delta \theta Δ θ δ λ \delta \lambda δ λ
棱镜对光束的限制作用相当于矩孔,它产生矩孔衍射。由光学笔记(二)知道,宽度为 a a a
Δ θ = λ / a \Delta \theta = \lambda /a
Δ θ = λ / a
从而棱镜的色分辨本领为
R ≡ λ δ λ = b d n d λ R \equiv \frac{\lambda}{\delta \lambda}=b \frac{\mathrm{d} n}{\mathrm{d} \lambda}
R ≡ δ λ λ = b d λ d n
设光栅第 k k k θ k \theta_k θ k Δ θ k \Delta \theta_k Δ θ k θ k + Δ θ k \theta_k+\Delta \theta_k θ k + Δ θ k
{ d sin θ k = k λ d sin ( θ k + Δ θ k ) = k λ + λ N ⟹ d cos θ k Δ θ k = λ N ⟹ Δ θ k = λ N d cos θ k \begin{cases} d \sin \theta_k = k \lambda \\ d\sin(\theta_k + \Delta \theta_k) = k\lambda+\frac{\lambda}{N}\end{cases} \Longrightarrow d \cos \theta_k \Delta \theta_k =\frac{\lambda}{N} \Longrightarrow \Delta\theta_k = \frac{\lambda}{Nd \cos \theta_k}
{ d sin θ k = k λ d sin ( θ k + Δ θ k ) = k λ + N λ ⟹ d cos θ k Δ θ k = N λ ⟹ Δ θ k = N d cos θ k λ
这就是光栅的半角宽度 表达式。进而由
δ λ = δ θ D θ = Δ θ D θ = d cos θ k ⋅ λ N d cos θ = λ k N \delta \lambda=\frac{\delta \theta}{D_{\theta}}=\frac{\Delta \theta}{D_{\theta}}=\frac{d \cos \theta}{k} \cdot \frac{\lambda}{N d \cos \theta} = \frac{\lambda}{kN}
δ λ = D θ δ θ = D θ Δ θ = k d cos θ ⋅ N d cos θ λ = k N λ
可得光栅的色分辨本领 为
R ≡ λ δ λ = k N R \equiv \frac{\lambda}{\delta \lambda}= kN
R ≡ δ λ λ = k N
得出结论:光栅的色分辨本领正比于衍射单元总数 N N N k k k d d d
FP干涉仪第 k k k
Δ i k = λ ε 4 π n h sin i k \Delta i_{k}=\frac{\lambda \varepsilon}{4 \pi n h \sin i_{k}}
Δ i k = 4 π n h sin i k λ ε
其中 ε \varepsilon ε δ λ \delta \lambda δ λ k k k δ i k \delta i_k δ i k
{ 2 n h cos i k = k λ 2 n h cos ( i k + δ i k ) = k ( λ + δ λ ) ⟹ δ i k ≈ k 2 n h sin i k δ λ \begin{cases} 2nh \cos i_k = k \lambda \\ 2nh \cos (i_k+\delta i_k) = k (\lambda + \delta \lambda) \end{cases} \Longrightarrow \delta i_k \approx \frac{k}{2nh \sin i_k} \delta \lambda
{ 2 n h cos i k = k λ 2 n h cos ( i k + δ i k ) = k ( λ + δ λ ) ⟹ δ i k ≈ 2 n h sin i k k δ λ
从而依照瑞利判据 δ i k = Δ i k \delta i_k = \Delta i_k δ i k = Δ i k δ λ \delta \lambda δ λ
λ ε 4 π n h sin i k = k 2 n h sin i k δ λ \frac{\lambda \varepsilon}{4 \pi n h \sin i_{k}} = \frac{k}{2nh \sin i_k} \delta \lambda
4 π n h sin i k λ ε = 2 n h sin i k k δ λ
δ λ = λ ε 2 π k = λ π k 1 − R R \delta \lambda = \frac{\lambda \varepsilon}{2 \pi k} = \frac{\lambda }{\pi k} \frac{1-R}{\sqrt{R}}
δ λ = 2 π k λ ε = π k λ R 1 − R
它恰好等于FP干涉仪的谱线宽度,但注意这其实是用两种完全不同的方法算出来的!
色分辨本领就是
λ δ λ = 2 π k ε = π k R 1 − R \frac{\lambda}{\delta \lambda} = \frac{2 \pi k}{\varepsilon}=\pi k \frac{\sqrt{R}}{1-R}
δ λ λ = ε 2 π k = π k 1 − R R
根据分光元件的机理,成像光谱仪可分为色散型 、干涉型 、滤光片型 、计算层析型 、编码孔径型 、三维成像型 成像光谱仪。
干涉型光谱仪具有高通量 、多通道 的优点。干涉型光谱仪与色散型光谱仪的信噪比之比为 ( S / N ) I ( S / N ) G = M 1 / 2 \frac{(S / N)_{I}}{(S / N)_{G}}=M^{1 / 2} ( S / N ) G ( S / N ) I = M 1 / 2 M M M
色散型成像光谱仪的光谱分辨率与狭缝宽度成反比。狭缝越窄,光谱分辨率越高。
色散型成像光谱仪的探测灵敏度与狭缝宽度成正比。狭缝越窄,进入系统的光通量越少,探测灵敏度越低。
干涉图:探测器接收到的信号强度 I I I Δ \Delta Δ I ( Δ ) I(\Delta) I ( Δ )
光谱图:探测器接收到的光谱强度 B B B σ \sigma σ B ( σ ) B(\sigma) B ( σ )
光谱:复色光经过色散系统分光后,强度按波长的大小依次排列的图案称为光谱。
干涉图和光谱图之间的 Fourier 变换关系为
B ( σ ) = ∫ − ∞ ∞ I ( Δ ) e − i 2 π σ Δ d Δ I ( Δ ) = ∫ − ∞ ∞ B ( σ ) e i 2 π σ Δ d σ B(\sigma)=\int_{-\infty}^{\infty} I(\Delta) \mathrm{e}^{-\mathrm{i} 2 \pi \sigma \Delta} \mathrm{d} \Delta \qquad I(\Delta)=\int_{-\infty}^{\infty} B(\sigma) \mathrm{e}^{\mathrm{i} 2 \pi \sigma \Delta} \mathrm{d} \sigma
B ( σ ) = ∫ − ∞ ∞ I ( Δ ) e − i 2 π σ Δ d Δ I ( Δ ) = ∫ − ∞ ∞ B ( σ ) e i 2 π σ Δ d σ
其中 σ \sigma σ Δ \Delta Δ I ( Δ ) = I R ( Δ ) − I R ( 0 ) / 2 I(\Delta) = I_{R}(\Delta)-I_{R}(0) / 2 I ( Δ ) = I R ( Δ ) − I R ( 0 ) / 2 B ( σ ) B(\sigma) B ( σ )
实数形式的 Fourier 变换关系为
B ( σ ) = ∫ 0 ∞ I ( Δ ) cos ( 2 π σ Δ ) d Δ I ( Δ ) = ∫ 0 ∞ B ( σ ) cos ( 2 π σ Δ ) d σ B(\sigma)=\int_{0}^{\infty} I(\Delta) \cos (2 \pi \sigma \Delta) \mathrm{d} \Delta \qquad I(\Delta)=\int_{0}^{\infty} B(\sigma) \cos (2 \pi \sigma \Delta) \mathrm{d} \sigma
B ( σ ) = ∫ 0 ∞ I ( Δ ) cos ( 2 π σ Δ ) d Δ I ( Δ ) = ∫ 0 ∞ B ( σ ) cos ( 2 π σ Δ ) d σ
干涉成像光谱技术从探测模式 上可以分为时间调制干涉成像光谱技术 ,空间调制干涉成像光谱技术 ,时空混合调制干涉成像光谱技术 。
基于迈克耳逊干涉仪的引力波探测器属于时间调制干涉成像光谱技术 。
成像光谱偏振仪结构包括调制模块 、干涉模块 、成像模块 。
成像光谱偏振仪可同时获取目标的二维空间信息 、一维光谱信息 、全偏振信息 。