光学笔记（二）波动光学基本原理

本文梳理一下波动光学的基本原理，插图主要来自钟锡华老师和赵凯华老师合编的《光学》。

定态光波

标量波与矢量波

波场中物理状态的扰动可用标量场描述的，称为标量波；需用矢量场描述的，称为矢量波。

矢量波可以有一个纵方向（与传播方向平行）的自由度和两个横方向（与传播方向垂直）的自由度。自由空间的电磁波是横波，它有两个自由度，它们对应着两个独立的偏振状态。自由空间电磁波是横波是 $\nabla \cdot \bm{E} =0$ 和 $\nabla \cdot \bm{B} = 0$ 决定的。

定态波场

当波列的持续时间比扰动的周期长得多时，可将光波当作无限长单色波列处理，这样的波在空间传播时形成定态波场。定态波场满足：

1. 空间各点的扰动是同频率的简谐振荡，频率与振源相同；
2. 波场中各点扰动的振幅不随时间变化，在空间形成一个稳定的振幅分布。

普遍的定态标量波的表达式为

$$U(\bm{x},t) = A(\bm{x})\mathrm{e}^{\mathrm{i}\varphi(\bm{x})} \mathrm{e}^{ - \mathrm{i} \omega t}$$

波面/等相位面是扰动的相位相等的各点的轨迹，在给定的时刻令 $\varphi(\bm{x}) = Const$ 得到一个曲面族，就是一个个等相面。

平面波与球面波

平面波波函数的特点是

1. 振幅 $A(\bm{x})$ 是常数，它与场点坐标无关；
2. 相位 $\varphi(\bm{x})$ 是直角坐标的线性函数，即 $\varphi(\bm{x}) = \bm{k} \cdot \bm{r} + \varphi_0 = k_x x+k_y y+k_z z+ \varphi_0$ 。

从而平面波的表达式为

$$U(\bm{x},t) = A \mathrm{e}^{\mathrm{i} \bm{k} \cdot \bm{r} - \mathrm{i} \omega t}$$

球面波波函数的特点为

1. 振幅 $A(\bm{x}) = A/r$ 反比于场点到振源的距离 $r$ ，这是能量守恒的要求；
2. 相位分布的形式为 $\varphi(\bm{x}) = k r+\varphi_0 = k |\bm{x}-\bm{x}^\prime| + \varphi_0$ 。

从而球面波的表达式为

$$U(\bm{x},t) = \frac{A}{r} \mathrm{e}^{\mathrm{i} k r - \mathrm{i} \omega t}$$

基本原理

波的叠加原理

当两列波同时存在时，在它们的交叠区域内每点的振动是各列波单独在该点产生的振动的合成，这就是波的叠加原理。

波的叠加原理既包括相干叠加，也包括非相干叠加。非相干光学系统是光强的线性系统，相干光学系统是复振幅的线性系统。

Note

波的叠加原理是指波场中各点振动的瞬时值满足线性叠加关系。对非相干波，线性叠加的结果反映为强度的线性叠加，干涉项被时间平均掉了；对相干波，线性叠加的结果，反映为复振幅的线性叠加，而强度一般不满足线性叠加关系。因此，无论是相干叠加还是非相干叠加，都是对波进行线性叠加的结果，两者都服从波的叠加原理。

惠更斯原理

波前 $\Sigma$上每个面元 $\mathrm{d}\Sigma$ 都可以看成是新的振动中心，它们发出次波，在空间某一点 $P$ 的振动是所有这些次波在该点的相干叠加。

/* 惠更斯原理明确了次波的叠加一定是相干叠加，由此可以构造分波前的干涉装置，例如最经典的杨氏双缝干涉实验。 */

干涉

相干条件

相干条件有三条：

1. 频率相同；
2. 存在相互平行的振动分量；
3. 相位差 $\delta$ 稳定。

为产生明显的高衬比度的干涉现象，尚有两个补充条件：

1. 振幅相差不悬殊
2. 光程差不能太大

第一个条件是由于衬比度的要求，第二个条件源于光场的时间相干性问题，见下面论证。

普通光源

对于普通光源，光的发射过程以自发辐射为主。这是一种随机过程，每个原子或分子先后发射的不同波列，以及不同原子或分子发射的各个波列，彼此之间在振动方向和相位上没有什么联系。因此普通光源发出的光具有以下特点：

• 扩展光源不同部分发光是独立的，没有固定的相位差，没有同一的振动方向；
• 光源发光过程在时间上是断续的，体现为发射许多断续的波列，持续时间 $\tau_0$ 比通常探测仪器的响应时间 $\Delta t$ 短得多。

为了解决第一个空间相干性问题，我们利用惠更斯原理构造了分波前干涉装置，将扩展光源在某处的总波，分成相互干涉的两部分；我们还可以利用分振幅干涉装置，将一束光的反射光和透射光分离，并进行自我干涉，规避了扩展光源不同部分发出的光的非相干性。

为了解决第二个时间相干性问题，我们要求分振幅之后的两列波在探测仪器处光程差不能太大，即第二个补充条件。这样可以保证探测仪器接收到的两列波来自同一个小波列。典例如迈克尔逊干涉仪。

干涉公式

设两列同频率简谐标量波为

$$\tilde{U}_1 = A_1 \mathrm{e}^{\mathrm{i}\varphi_1} \qquad \tilde{U}_2 = A_2 \mathrm{e}^{\mathrm{i}\varphi_2}$$

其中时谐因子 $\exp(\mathrm{i} \omega t)$ 已经略去，那么两列波在同一处的相干叠加为

$$\tilde{U} = \tilde{U}_1 + \tilde{U}_2 =A_1 \mathrm{e}^{\mathrm{i}\varphi_1} + A_2 \mathrm{e}^{\mathrm{i}\varphi_2}$$

则可算得叠加后的光强为

$$I = \tilde{U} \tilde{U}^*= I_1 +I_2 + 2\sqrt{I_1 I_2} \cos(\varphi_1 - \varphi_2)$$

定义 $I_0 = I_1+I_2$ ，相位差 $\delta = \varphi_1 - \varphi_2$ ，衬比度

$$\gamma = \frac{I_{\text{max}} - I_{\text{min}}}{I_{\text{max}} + I_{\text{min}}}$$

则当 $\delta = k\pi$ 时，叠加光强公式可以写成

$$I = I_0 (1+\gamma \cos \delta)$$

一般情况下不可以！

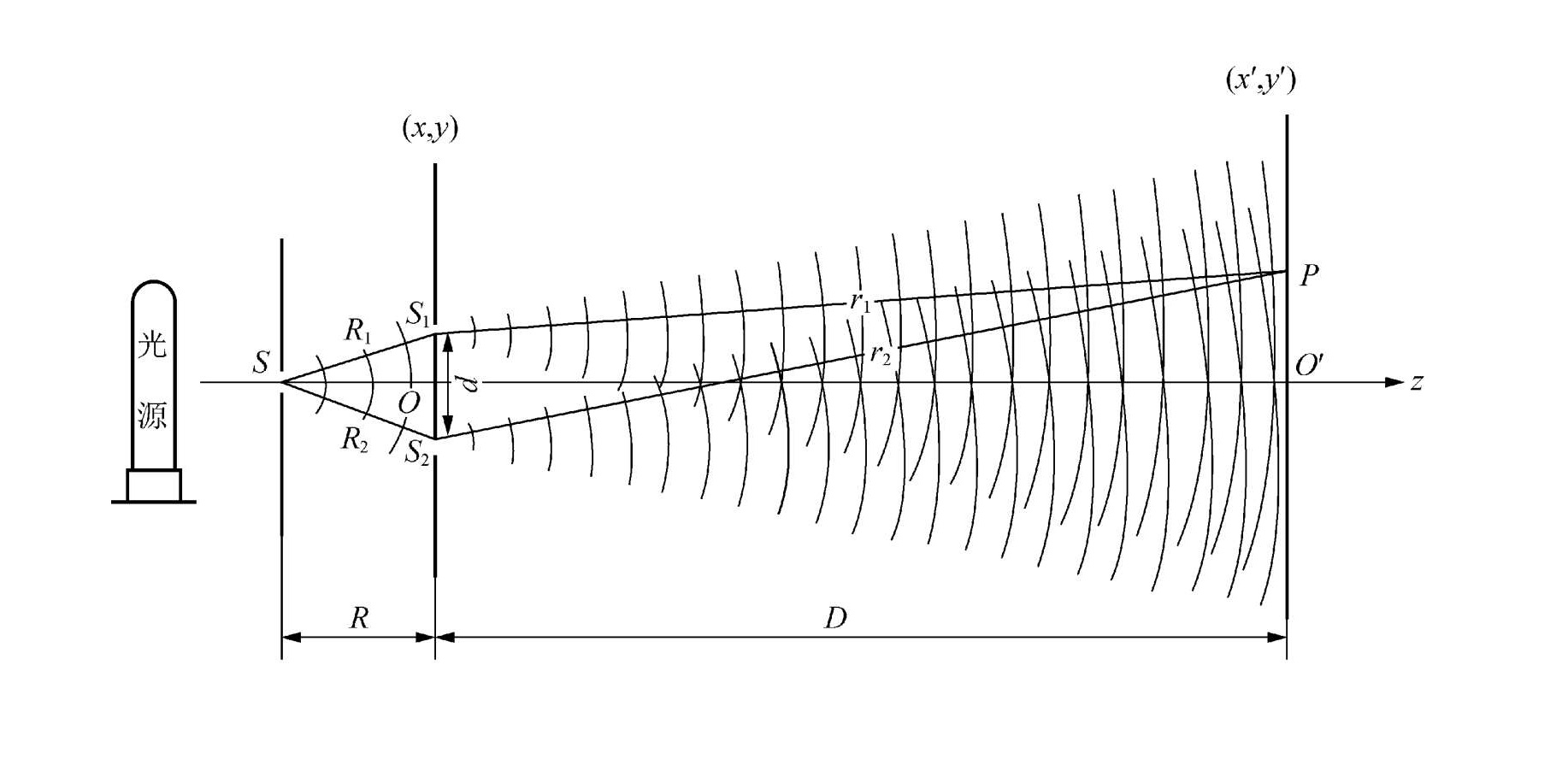
双缝干涉

干涉装置如图所示。

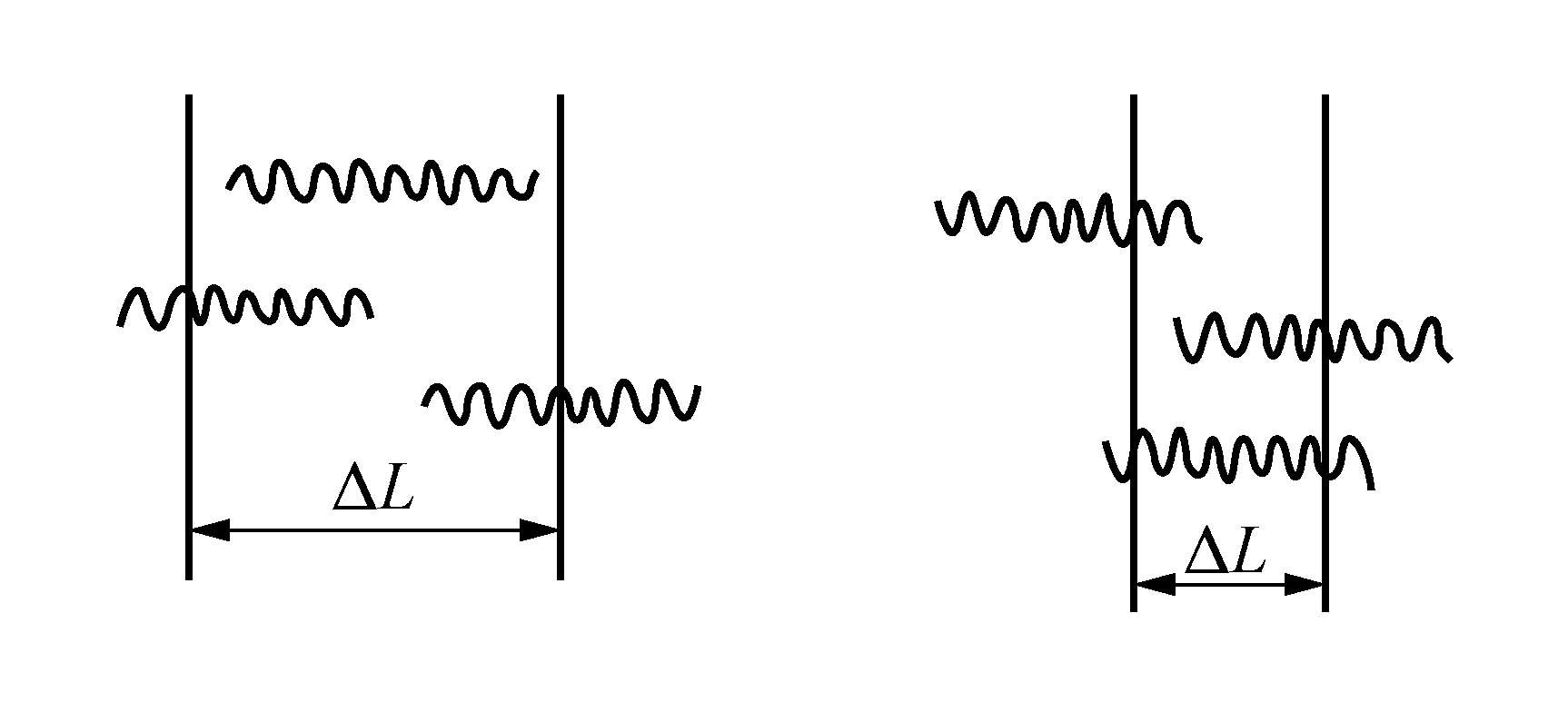
干涉条纹的间距定义为两条相邻亮纹或两条暗纹之间的距离，公式为

$$\Delta x = \frac{\lambda D}{d}$$

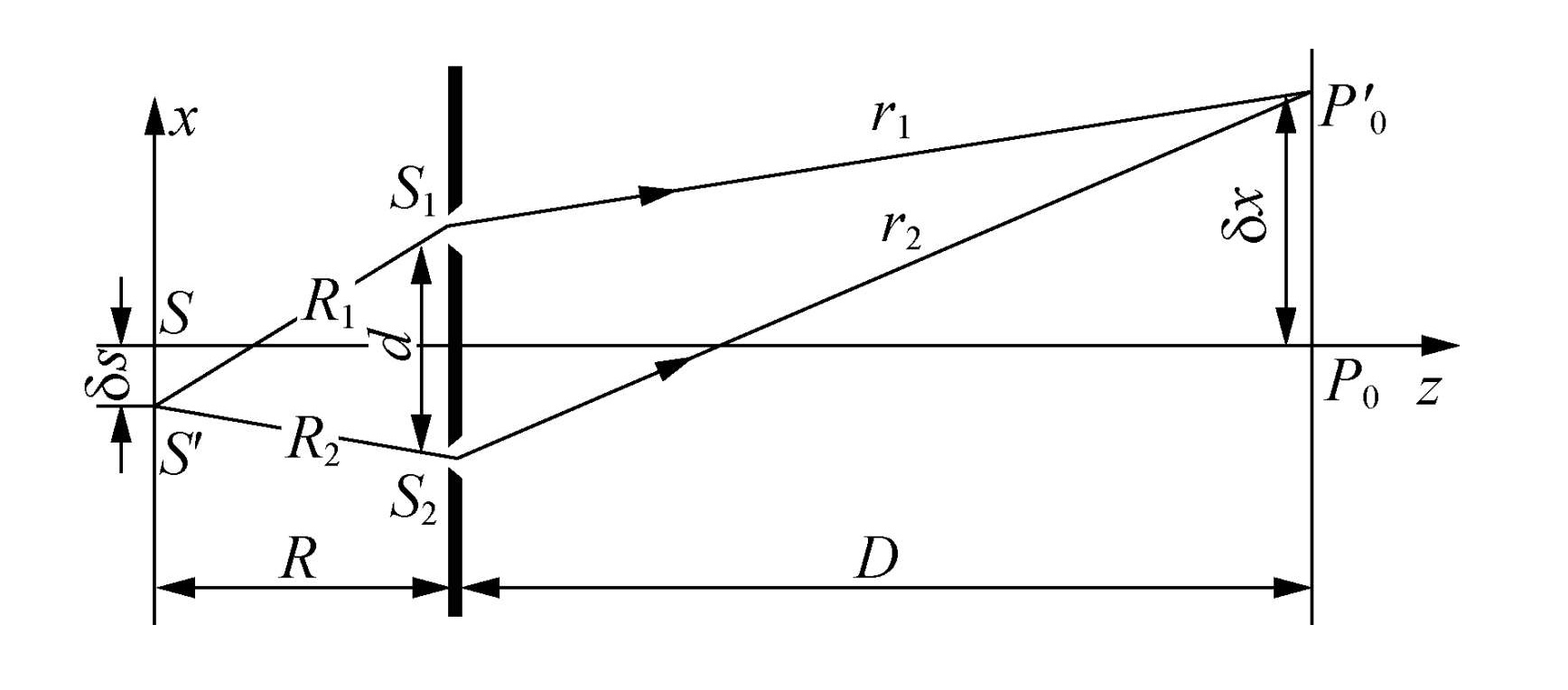
条纹位移与点源位移的关系为 $\delta x = \frac{D}{R} \delta s$，移动方向相反，如图所示。

空间相干性

杨氏双缝干涉中，光源的极限宽度 $b$ 为

$$b \approx \frac{R}{D} \frac{\lambda D}{d} \approx \frac{R\lambda}{d}$$

即要求光源的两端作为点源，在衍射屏上产生的条纹位移恰好等于干涉条纹间距。再延长光源，则开始经历空间周期，明暗相互抵消。

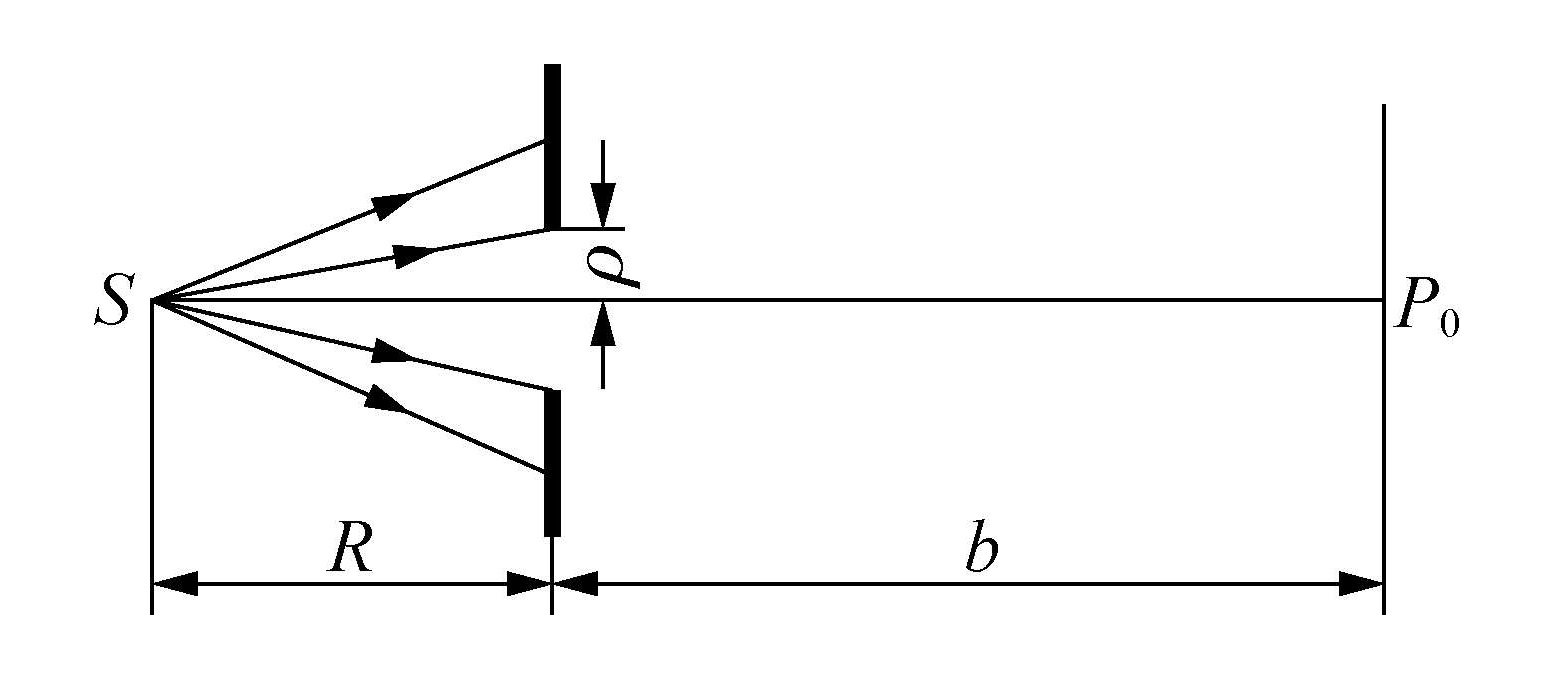
现在我们可以从具体的干涉装置中解脱出来，倒过来提问题：给定宽度为 $b$ 的面光源，在它的照明空间中在波前上多大的范围里提取出来的两个次波源 $S_1$ 和 $S_2$ 还是相干的？作如图所示示意图。

这便是所谓的光场空间相干性问题。为了解决此问题，只需要将极限宽度的表达式倒过来写就可以了

$$d \approx \frac{R \lambda}{b}$$

这式中的 $d$ 给出了光场中相干范围的横向线度。定义 $S_1,S_2$ 对光源中心所张的角度为 $\Delta \theta_0 = d /R$ ，以此来表征相干范围，称为相干范围的孔径角，从而可得公式

$$b \Delta \theta_{0} \approx \lambda$$

上述两个公式称为空间相干性的反比公式。

衍射

Kirchoff积分公式

Kirchoff积分公式是标量衍射理论的核心，推导参见电动力学，这里直接给出

$$\psi(\bm{x}) = -\frac{1}{4\pi} \int_{S_1} \frac{\mathrm{e}^{\mathrm{i} kr}}{r} \left[\nabla^{\prime} \psi(\bm{x}^{\prime}) + \left( \mathrm{i} k - \frac{1}{r} \right) \frac{\bm{r}}{r} \psi(\bm{x}^{\prime}) \right] \cdot \bm{n}^{\prime} \, \mathrm{d} \bm{S}^{\prime}$$

对于点波源，$\psi(\bm{x}^{\prime}) = \psi_0\mathrm{e}^{\mathrm{i} kx^\prime}/x^\prime$ ，上式退化成Fresnel衍射公式

$$\psi(\bm{x}) = -\frac{\mathrm{i}\psi_0}{2\lambda} \int_{S_1} \frac{\mathrm{e}^{\mathrm{i} k(r+x^\prime)}}{rx^\prime} \left(\cos \theta_0 + \cos \theta \right) \mathrm{d} S^{\prime}$$

其中 $\theta_0$ 为孔面法向矢量 $\bm{n}^{\prime}$ 与 $\bm{x}^\prime$ 的夹角，$\theta$ 为孔面法向矢量 $\bm{n}^{\prime}$ 与 $\bm{r}$ 的夹角。

衍射分类

• 菲涅尔衍射：衍射屏距光源和接收屏均为有限远，或者说入射波和衍射波都是球面波
• 夫琅禾费衍射：衍射屏距光源和接收屏均为无限远，即入射波和衍射波都可看作是平面波

点光源的Fresnel衍射

实验装置

其中涉及到的物理量如下表所示

物理量	数量级
圆孔半径 $\rho$	毫米
光源到圆孔的距离 $R$	米
接收屏幕到圆孔的距离 $b$	3米到5米

Fresnel半波带法

适用条件：只适用于能整分成整数个半波带的情况，只能求菲涅尔衍射中心场点的光强。

原理：相邻半波带到 $P$ 点的光程差为 $\lambda/2$ ，振幅相近，应用Fresnel衍射公式并作近似可得

振幅公式

• 圆孔衍射：设共有 $n$ 个半波带，中心场点振幅为 $A(P_0) = \frac{1}{2} \left[A_1 + (-1)^{n+1} A_n \right]$ ，偶数暗奇数亮。
• 圆屏衍射：遮住前 $k$ 个半波带，则中心场点振幅为 $A(P_0) = A_{k+1} /2$ ，中心总是亮的，即所谓泊松亮斑。

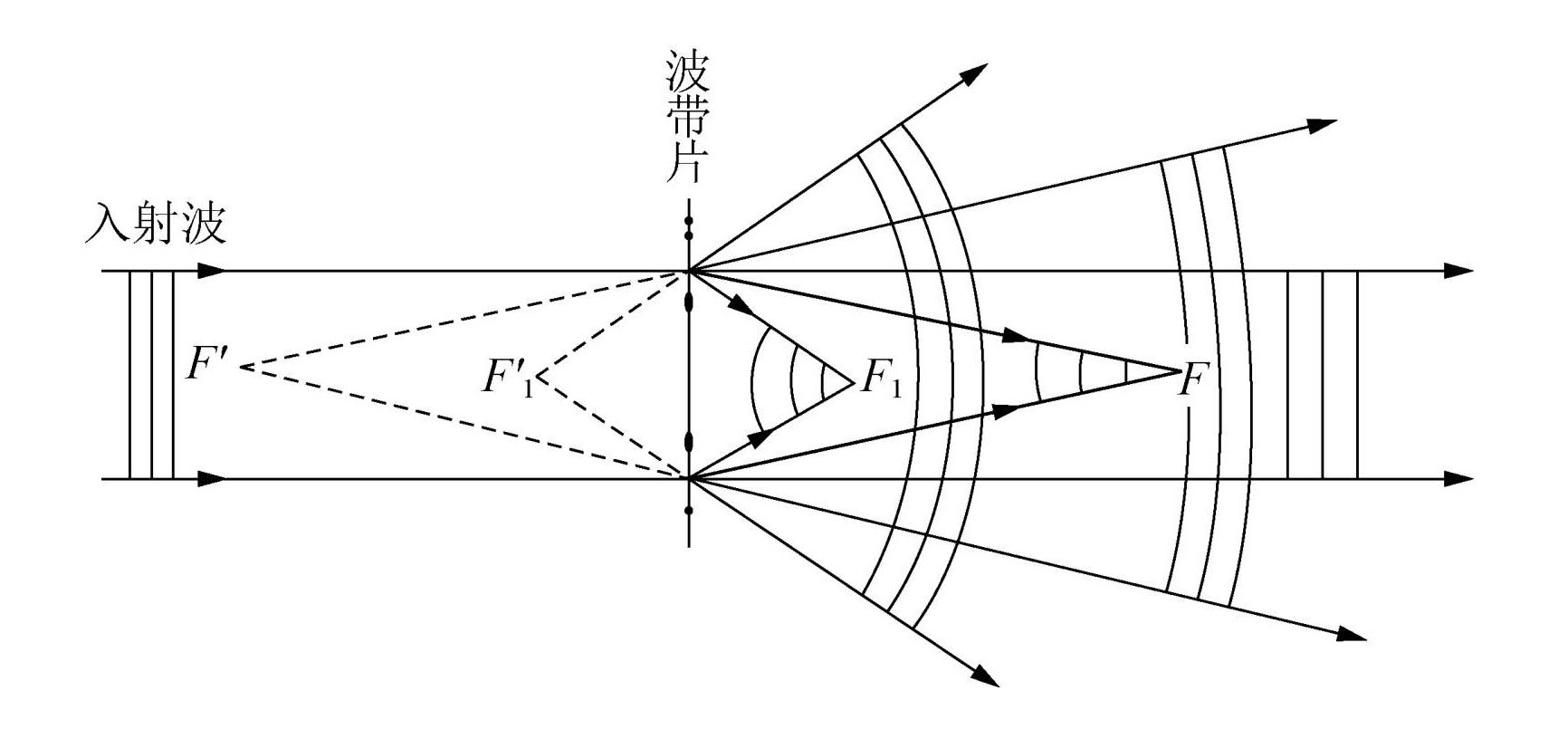
Fresnel波带片

由简单的计算可知，第 $k$ 个半波带的半径为

$$\rho_{k}=\sqrt{\frac{R b}{R+b} k \lambda}=\sqrt{k} \rho_{1}$$

其中 $\rho_{1}$ 为第一个半波带的半径。

因此若将偶数或奇数的半波带涂黑，这就构成一块波带片，称为Fresnel波带片，它可使轴上一定距离的场点光强增加很多倍。

Fresnel波带片可视为一个透镜。改写第 $k$ 个半波带半径公式，得到

$$\frac{1}{R}+\frac{1}{b}=\frac{k \lambda}{\rho_{k}^{2}}$$

定义 $f = \rho_{k}^{2} / k \lambda$，便得到透镜成像公式。

应当注意，波带片与透镜有个重要区别，即一个波带片有许多焦点，上面给出的是它的主焦点，除此之外，还有一系列次焦点，它们的距离分别是 $f/3,f/5,f/7,\cdots$ 。当平行光照明时，在轴上这些位置处也会出现亮点。请读者自行思考，然后查看说明。

Note

以 $b =f/3$ 为例，代入$f = \rho_{k}^{2} / k \lambda$，得到此时波带片所含的半波带个数为

$$k^\prime = 3k$$

即半波带数增加三倍。这说明原来波带片中每一个透光的半波带，相对于 $b=f/3$ 处来说，变成为三个半波带，其中有两个分别为奇数和偶数的半波带。它们对场点的贡献相互抵消，有贡献的只是剩下的一个半波带。波带中透光部分所有有贡献的半波带在轴上场点处合成振幅的再叠加是同相叠加，因此形成亮点，即证明了 $b=f/3$ 处为一个次焦点。同理可以证明，$b=f/5,f/7,\cdots$ 处均为次焦点。

此外，每块波带片除有几个实焦点外，在对称的位置上还存在一系列虚焦点。菲涅耳波带片是有多个虚、实焦点这一事实告诉我们，它所产生的衍射场虽很复杂，但它包含有一系列会聚的和发散的球面波成分，当然还有按几何光学规律直进的平面波成分。

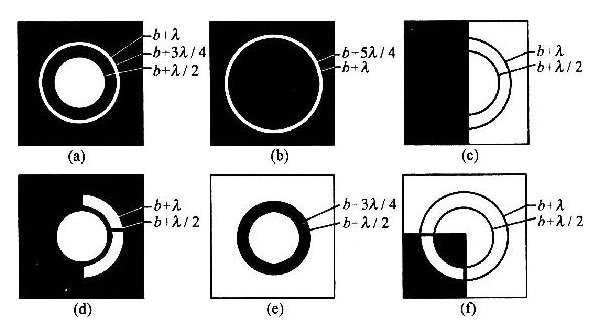
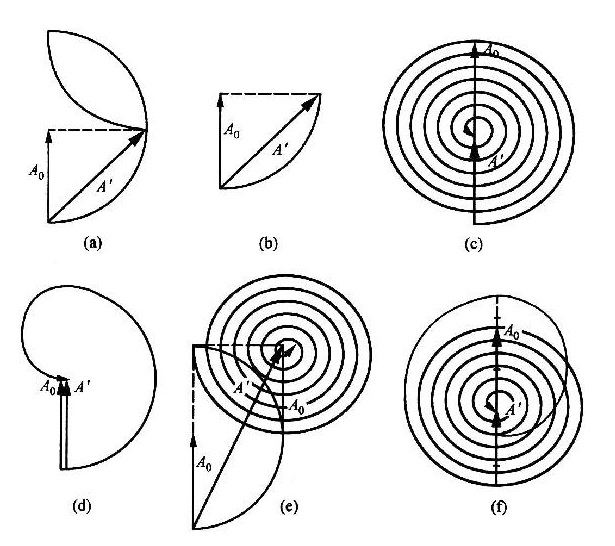
矢量图法

无穷细的分割波前，可讨论任意非整数个裸露波带情况。每个半波带对应1/2圈。扇形遮挡后，改变振幅，而非强度。

以上是一道经典例题，不言自明。

夫琅禾费衍射

单缝衍射

用矢量图法或Kirchoff积分公式，可以得到单缝衍射公式

$$I = I_0 \left( \frac{\sin\alpha}{\alpha} \right)^2$$

其中 $\alpha = \pi a \sin \theta / \lambda$ ，$\theta$ 为衍射角。

令 $\sin \alpha=0$ ，即 $\alpha = k\pi$ ，即 $\sin \theta_k = k\lambda /a$ ，可得第 $k$ 级暗条纹对应的衍射角 $\theta_k \approx \sin \theta_k = k\lambda /a$ 。

但 $\alpha \to 0\pi$ 时，$I \to I_0$ 为中央主极大。中央主极大的半角宽度为 $\lambda/a$ 。

由 $I$ 的极值条件

$$\frac{\mathrm{d}}{\mathrm{d}\alpha} \left( \frac{\sin\alpha}{\alpha} \right)=0 \Longrightarrow\alpha = \tan \alpha$$

可算得第 $k$ 级亮条纹对应的衍射角

$$\sin \theta_1=\pm 1.43 \frac{\lambda}{a}, \ \sin \theta_2=\pm 2.46 \frac{\lambda}{a}, \ \sin \theta_3=\pm 3.47 \frac{\lambda}{a}, \ \cdots$$

矩孔衍射

夫琅禾费矩孔衍射为两方向的单缝衍射因子相乘，即

$$I = I_0 \left( \frac{\sin\alpha}{\alpha} \right)^2 \left( \frac{\sin\beta}{\beta} \right)^2$$

其中 $\alpha = \dfrac{\pi a \sin \theta_1}{\lambda},\ \beta = \dfrac{\pi b \sin \theta_2}{\lambda}$ ，$\theta_1, \theta_2$ 为出射波波矢的方向角。

圆孔衍射

圆孔衍射公式为

$$I=I_{0}\left[\frac{2 J_{1}\left(k a \sin \theta\right)}{k a \sin \theta}\right]^{2}$$

其中 $J_1$ 为一阶Bessel函数。

圆孔衍射的中央亮斑称为艾里斑，约占总光强的84%。由一阶Bessel函数的零点可知其角半径为

$$\Delta \theta = \frac{1.22\lambda}{D}$$

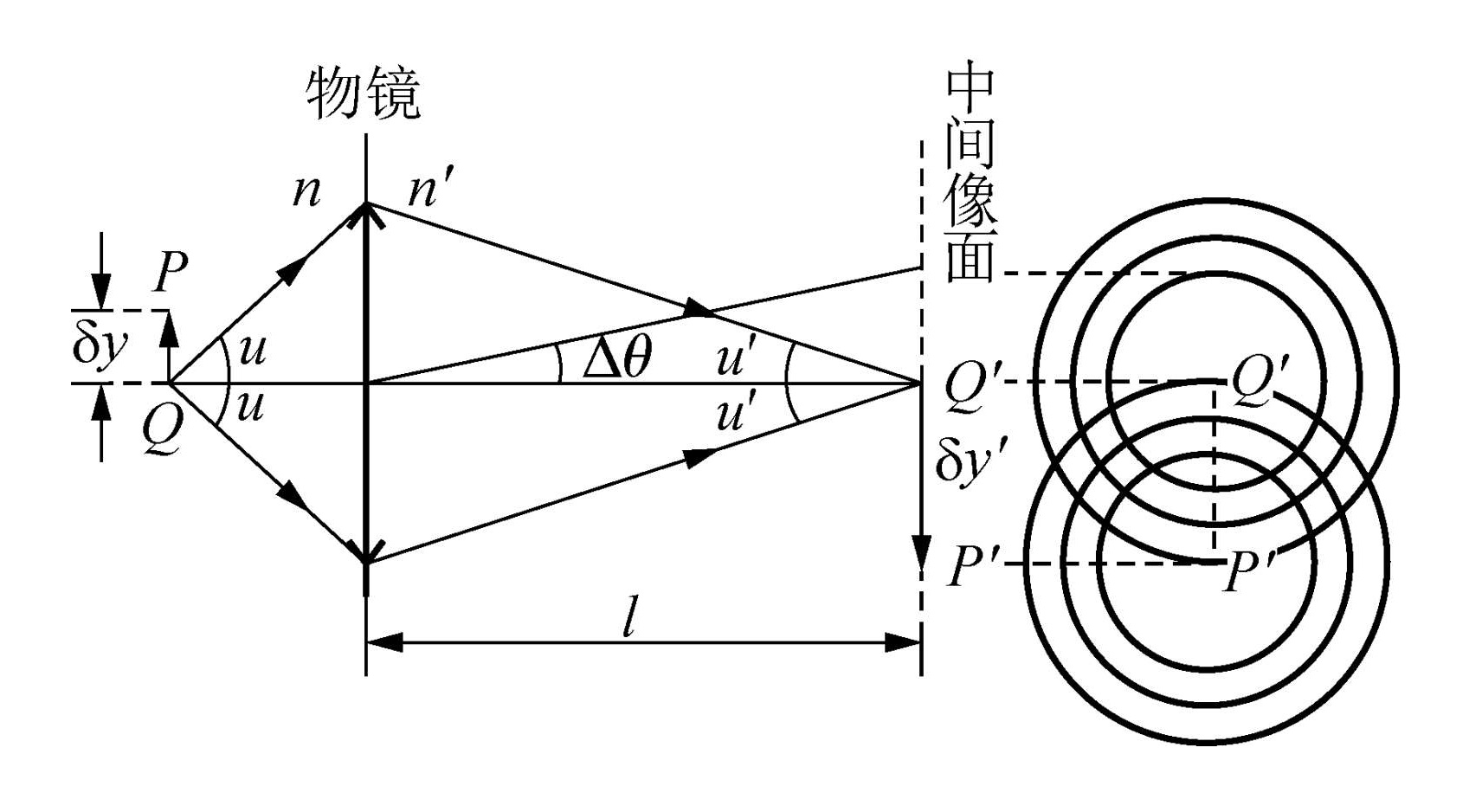
其中 $D =2a$ 为圆孔直径。由此，可以规定光学仪器的最小分辨角：当两个像之间的角距离等于艾里斑的角半径时恰好能分清，角距离再小就分不清了，从而

$$\delta \theta_\text{m} = \frac{1.22\lambda}{D}$$

人眼的最小分辨角为 $\delta \theta_\text{e} =1^\prime$ 。望远镜和放大镜的最小分辨角应当巧妙设计，使得仪器的最小分辨角 $\delta \theta_\text{m}$ 乘视角放大率 $M$ 恰好等于人眼的最小分辨角 $\delta \theta_\text{e}$ 。

/* 如果视角放大率使得乘积大于人眼最小分辨角，不能使像变得更加清晰，因为仪器那一步已经限制了最小辨识能力，视角放大仅仅是把模糊的像放大；如果视角放大率使得乘积小于人眼最小分辨角，那就亏了，本来光学仪器能分辨清楚的，由于视角放的不够大到人眼里反而分不清了。*/

显微镜的分辨本领不用最小分辨角而用最小分辨距离来衡量

$$\delta y_{\mathrm{m}}=\frac{0.61 \lambda}{n \sin u} = \frac{0.61 \lambda}{\text{N.A.}}$$

其中 $n \sin u$ 称为数值孔径，用 $\text{N.A.}$ 表示。