光学笔记（一）几何光学

本文梳理一下几何光学中重要的模型和公式，插图主要来自钟锡华老师和赵凯华老师合编的《光学》。由于中学物理竞赛时已经学得比较扎实，因此此处主要重心在公式的罗列，以及理想光具组成像上。

几何光学基本定律

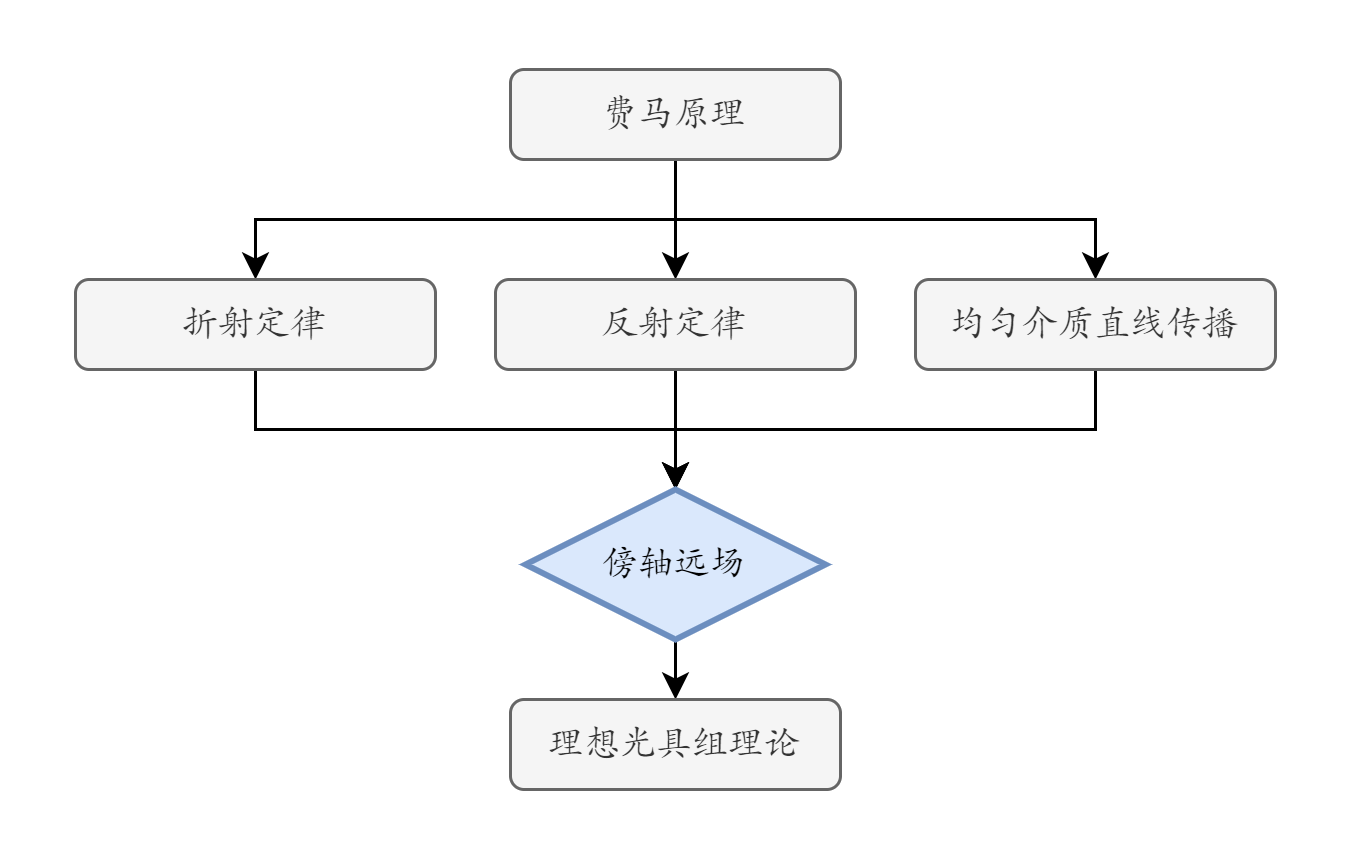
几何光学的基本架构如下

当光的波长可视为极短，从而其波动效应不明显时，人们把光的能量看成是沿着一根根光线传播的，它们遵从直进、反射、折射等定律，这便是几何光学。

费马原理

基本概念

1. 光速：光在介质中的传播速度为 $v=c/n$ 。

   /* 此速度为随介质运动的参考系中，观察者看到的光的传播速度 */

2. 光程：光在介质内的光程定义为 $\Delta = \displaystyle\int n \,\mathrm{d} l$ 。

3. 费马原理：光线的实际路径上，光程的变分为 $0$，即 $\displaystyle \delta \int_L n \,\mathrm{d} l = 0$ 。

虚光程

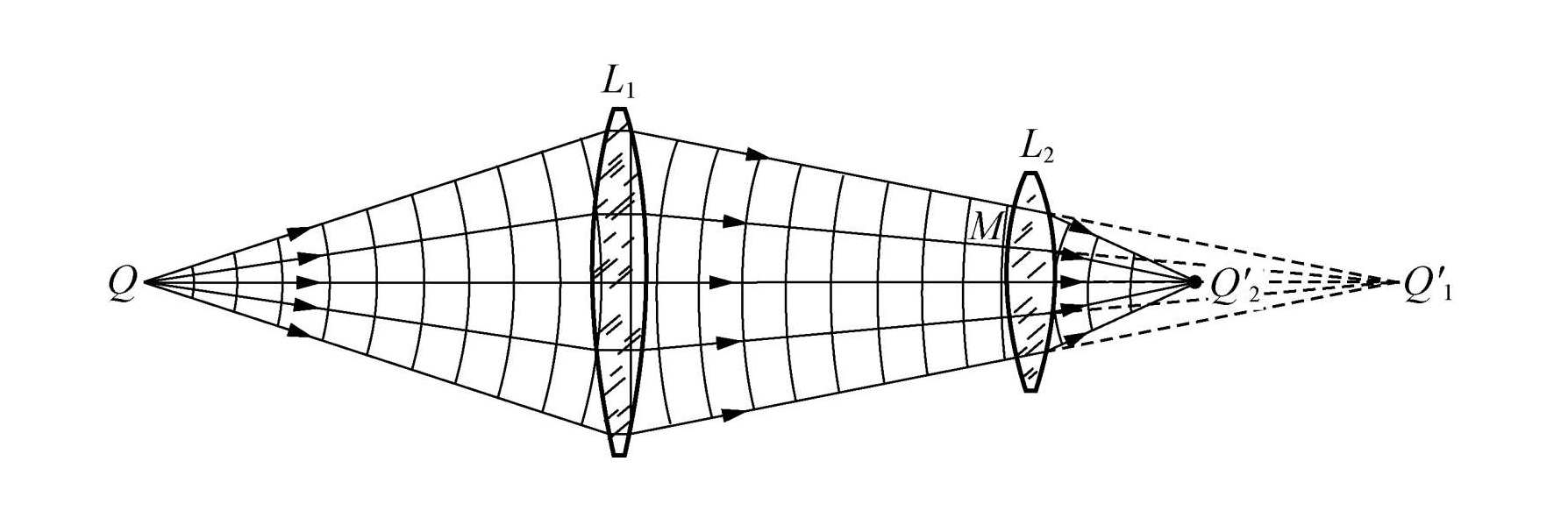
虚光程为光线延长线的光程，实际并不存在，因此应该取负数。在如图所示系统中，光程为

$$\Delta=Q Q_{1}^{\prime}-Q_{1}^{\prime} M+Q_{2}^{\prime} M$$

基本定律

由费马原理可导出几何光学三个基本定律：

1. 光在均匀介质中沿着直线传播
2. 反射定律 $i=i^{\prime}$
3. 折射定律 $n_1 \sin i_1 = n_2 \sin i_2$

成像

基本原理

等光程性：物像之间所有光线光程相等。

光路可逆：如果从物点 $P$ 发出的光线经光学系统后在 $Q$ 点成像，则 $Q$ 点发出的光线经同一系统后必在 $P$ 点成像，即物像之间是共轭的。

常见光具

球面透射镜：物方像方异侧，$\Phi=\dfrac{n^{\prime}-n}{r}$

平面反射镜：物方像方同侧，$\Phi=0$

球面反射镜：物方像方同侧，$\Phi=-\dfrac{2n}{r}$

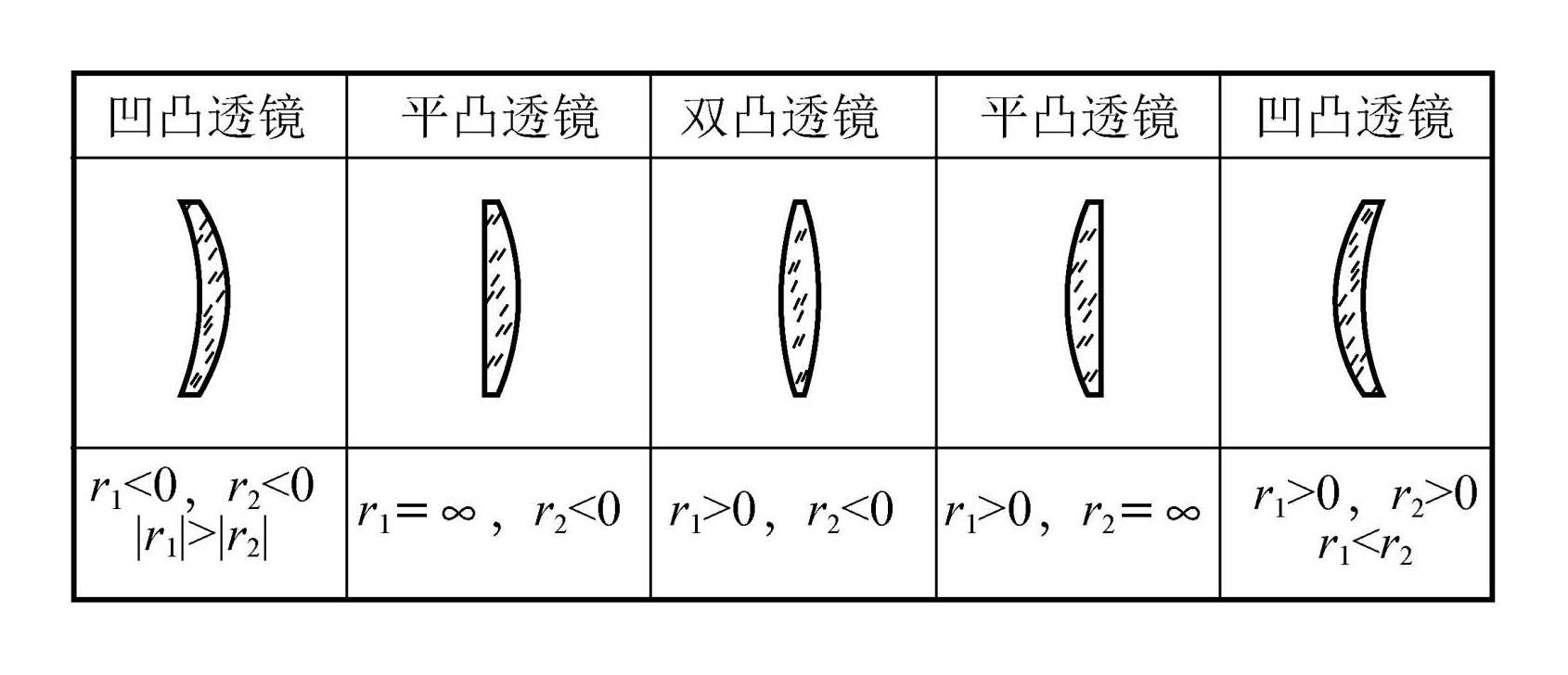
光心重合时，光焦度直接相加，典型例子为薄透镜，它是两个密接的折射球面，其光焦度为

$$\Phi=\frac{n_{L}-n}{r_{1}}+\frac{n^{\prime}-n_{L}}{r_{2}}$$

高斯成像

高斯成像的核心公式为

$$\frac{n}{s}+\frac{n^{\prime}}{s^{\prime}}=\Phi$$

其符号法则如下

• 对于物距 $s$ ，实物为正，虚物为负
• 对于像距 $s^{\prime}$ ，实像为正，虚像为负
• 对于半径 $r$ ，凸球为正，凹球为负

像的横向放大率为

$$V = - \frac{n s^{\prime}}{n^{\prime} s}$$

其符号法则如下

• $V>0$ 像正立，$V<0$ 像倒立
• $|V|>1$ 像放大，$|V|<1$ 像缩小

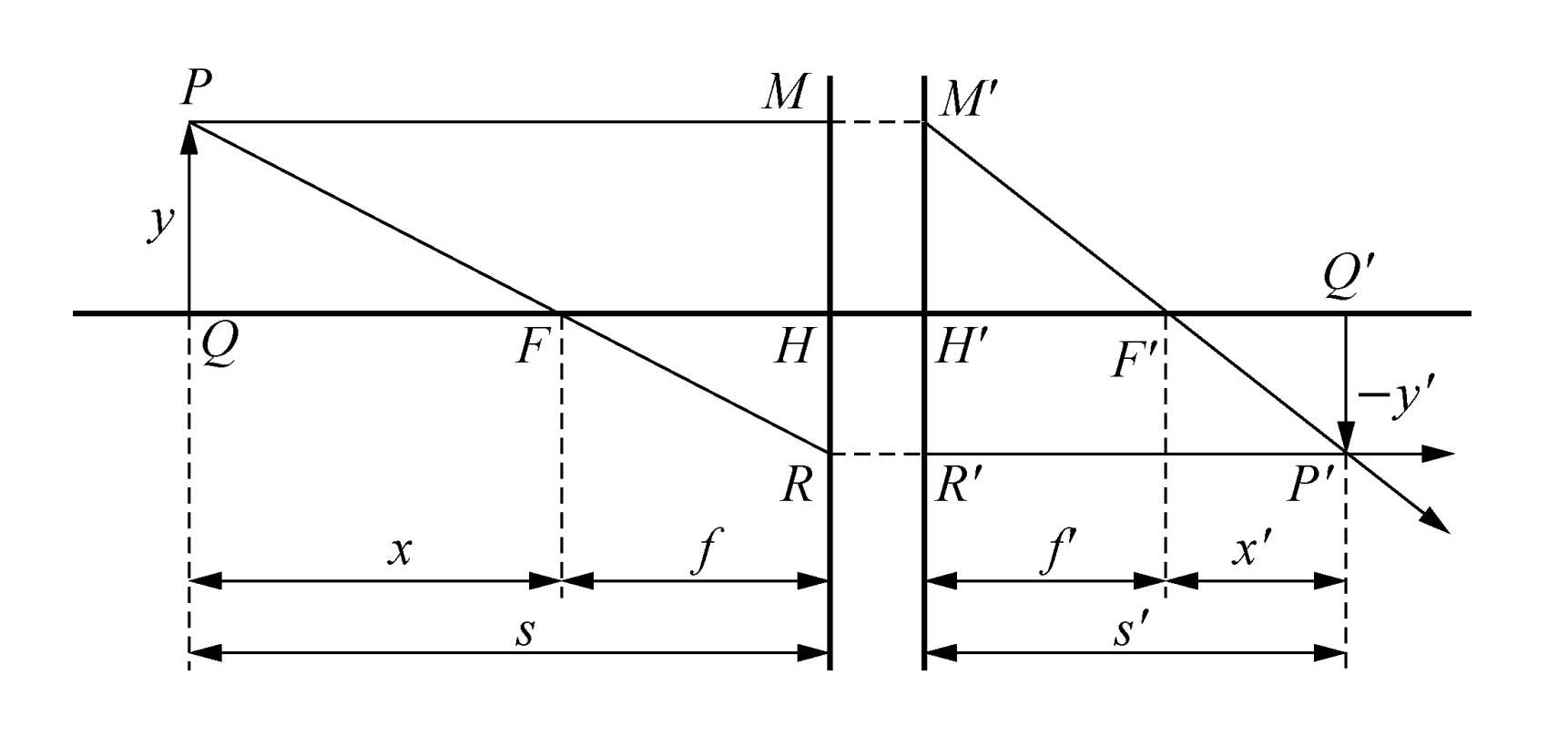
牛顿成像

牛顿成像的核心公式为

$$xx^\prime = f f^\prime$$

其符号法则如下

• 物方焦距定义为 $f=n/\Phi$ ，像方焦距定义为 $f^{\prime} = n^{\prime} / \Phi$
• 物点在物方焦点 $F$ 之左，$x>0$ ；物点在物方焦点 $F$ 之右，$x<0$
• 像点在像方焦点 $F^{\prime}$ 之左，$x^{\prime}>0$ ；物点在物方焦点 $F^{\prime}$ 之右，$x^{\prime}<0$

像的横向放大率为

$$V = -\frac{f}{x} = -\frac{x^{\prime}}{f^{\prime}}$$

其符号法则如下

• $V>0$ 像正立，$V<0$ 像倒立
• $|V|>1$ 像放大，$|V|<1$ 像缩小

特殊光具

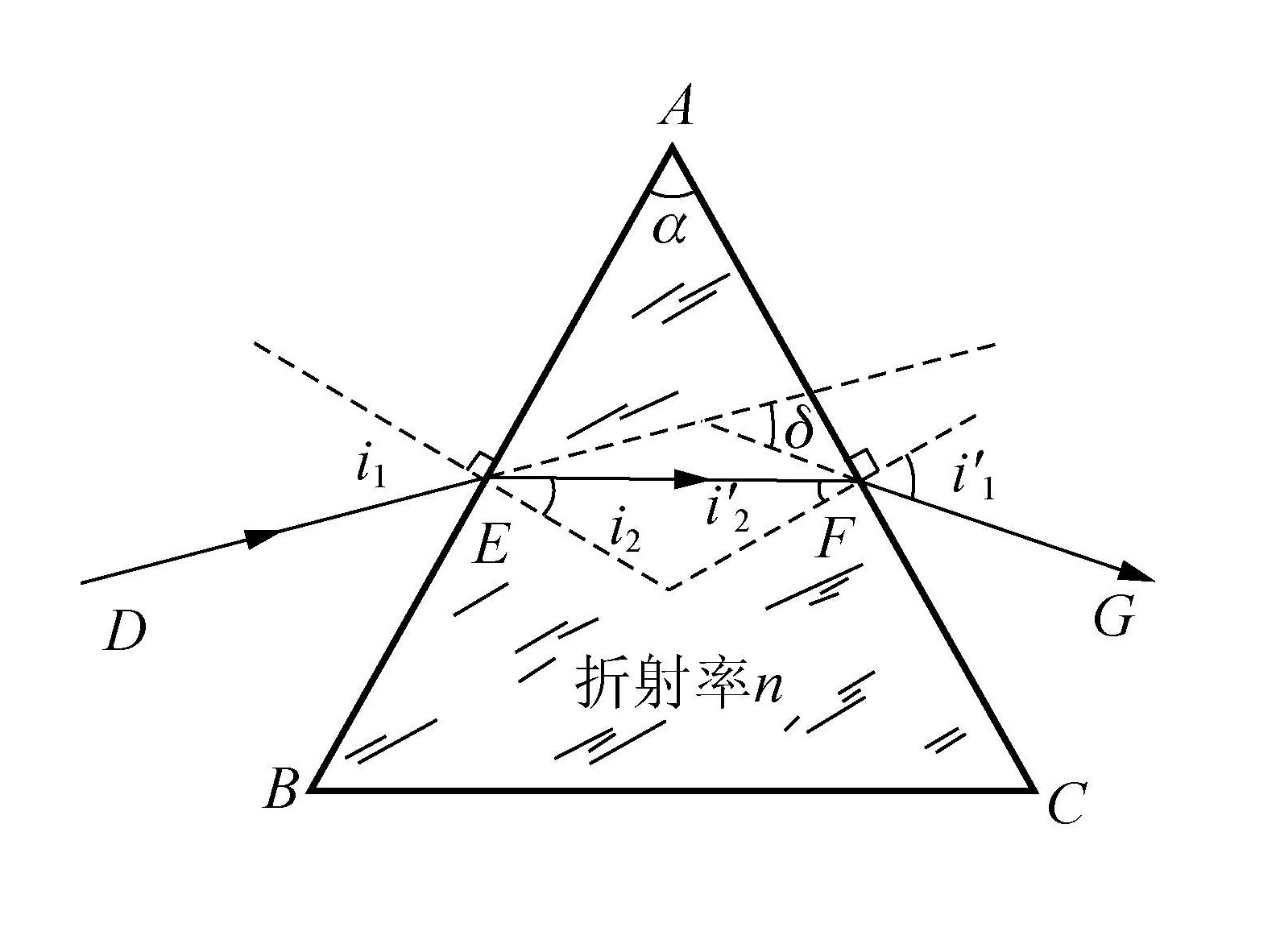
棱镜

棱镜的最小偏向角 $\delta_m$ 满足

$$n=\frac{\sin \frac{\alpha+\delta_m}{2}}{\sin \frac{\alpha}{2}}$$

产生最小偏向角的充要条件是光线相对于棱镜对称，即

$$i_1 = i^{\prime}_1 \qquad i_2 = i^{\prime}_2$$

此条件可通过光路可逆性推知。

光楔

光楔可认为是厚度很小的三棱镜。经光楔成像后，像仍在物的位置，但向楔尖方向移动

$$\Delta y =(n-1) \alpha s$$

其中 $\alpha$ 为光楔的顶角。

理想光具组理论

焦点和焦面

焦点和焦面的定义与前面引入的相同，即与无穷远像平面共轭的为物方焦面，其轴上点是为物方焦点，记作 $F$ ；与无穷远物平面共轭的为像方焦面，其轴上点是为像方焦点，记作 $F^\prime$ 。

望远系统没有焦点和焦面。

主点和主面

横向放大率等于1的一对共轭面，叫做主面。属于物方的叫物方主面，其轴上点叫做物方主点，记作 $H$ ；属于像方的叫像方主面，其轴上点叫做像方主点，记作 $H^\prime$ 。

主点和焦点统称为理想光具组的基点，主面和焦面统称为理想光具组的基面。

物像关系

给定了主面和焦点，便可以求物像关系。其核心公式为高斯公式

$$\frac{f^{\prime}}{s^{\prime}}+\frac{f}{s}=1$$

或牛顿公式

$$xx^\prime = f f^\prime$$

符号约定为

• 物点/物方焦点在物方主点 $H$ 之左，$s>0$ / $f>0$ ；物点/物方焦点在物方主点 $H$ 之右，$s<0$ / $f<0$ ；
• 像点/像方焦点在像方主点 $H^\prime$ 之左，$s^\prime<0$ / $f^\prime<0$ ；像点/像方焦点在像方主点 $H^\prime$ 之右，$s^\prime>0$ / $f^\prime>0$ 。
• 物点在物方焦点 $F$ 之左，$x>0$ ；物点在物方焦点 $F$ 之右，$x<0$
• 像点在像方焦点 $F^{\prime}$ 之左，$x^{\prime}>0$ ；物点在物方焦点 $F^{\prime}$ 之右，$x^{\prime}<0$

总而言之，$x$ 以焦点 $F$ 为判据，$s$ 和 $f$ 都以主点为判据。

横向放大率公式为

像的横向放大率为

$$V = -\frac{f}{x} = -\frac{x^{\prime}}{f^{\prime}} = -\frac{f s^\prime}{f^\prime s}$$

角放大率定义为共轭光线与光轴夹角的正切之比

$$W = \frac{\tan u^\prime}{\tan u} = -\frac{s}{s^\prime}$$

从而有

$$VW = \frac{f}{f^\prime}$$

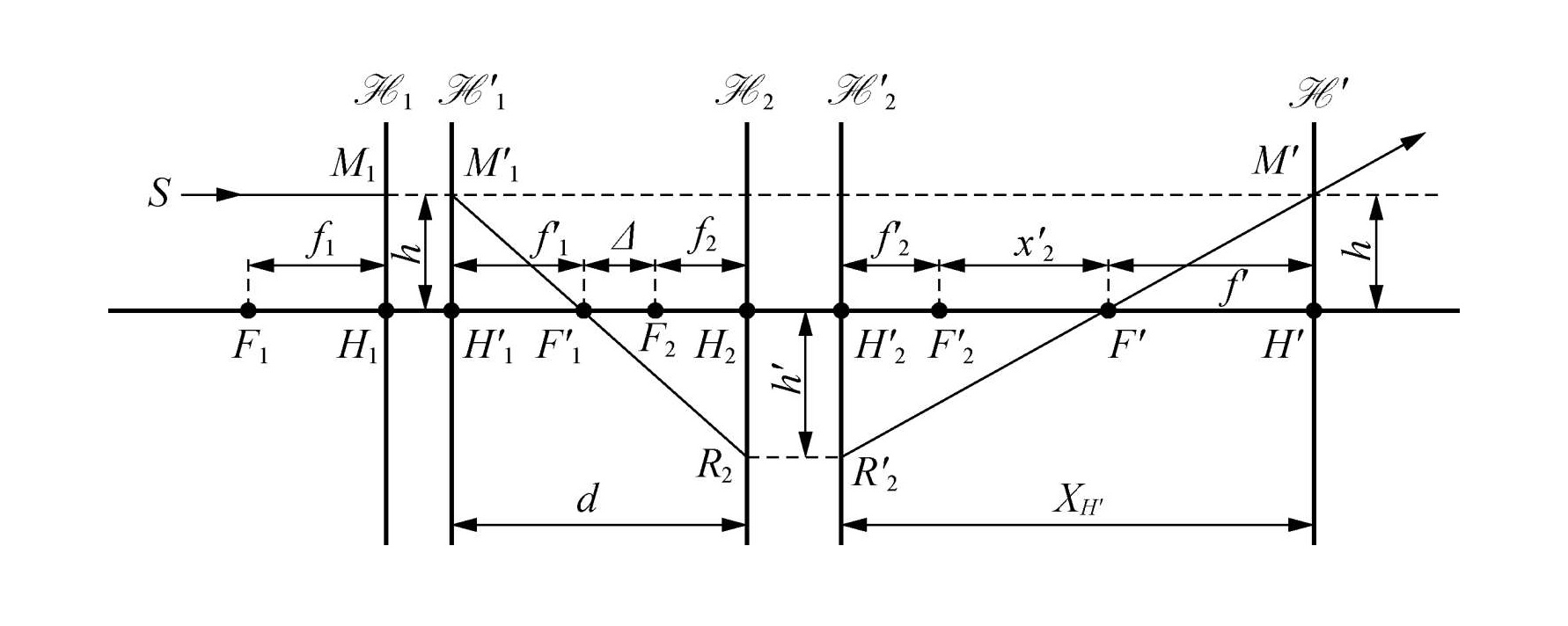
理想光具组的联合

理想光具组联合的目标是，给定光具组1和光具组2的基点 $F_1,F_2,H_1,H_2,F_1^\prime, F_2^\prime, H_1^\prime , H_2^\prime$ 与基面，以及两光具组之间的距离，求它们联合起来作为一个光具组时的基点，基面。作符号约定为

符号	意义	说明
$\Delta$	$F_1^\prime$ 与 $F_2$ 之间的距离	无
$d$	$H_1^\prime$ 与 $H_2$ 之间的距离	$d=f_1^\prime + \Delta +f_2$
$X_H$	联合光具组物方主点 $H$ 与 $H_1$ 之间的距离	$H$ 在 $H_1$ 左边则 $X_H>0$
$X_H^\prime$	联合光具组像方主点 $H^\prime$ 与 $H_2^\prime$ 之间的距离	$H^\prime$ 在 $H_2^\prime$ 右边则 $X_H^\prime >0$

联合公式为

$$f = -\frac{f_1 f_2}{\Delta} \qquad f^\prime = -\frac{f_1^\prime f_2^\prime}{\Delta}$$

$$X_H = f_1 \frac{d}{\Delta} \qquad X_H^\prime = f_2^\prime \frac{d}{\Delta}$$

光学仪器

眼睛

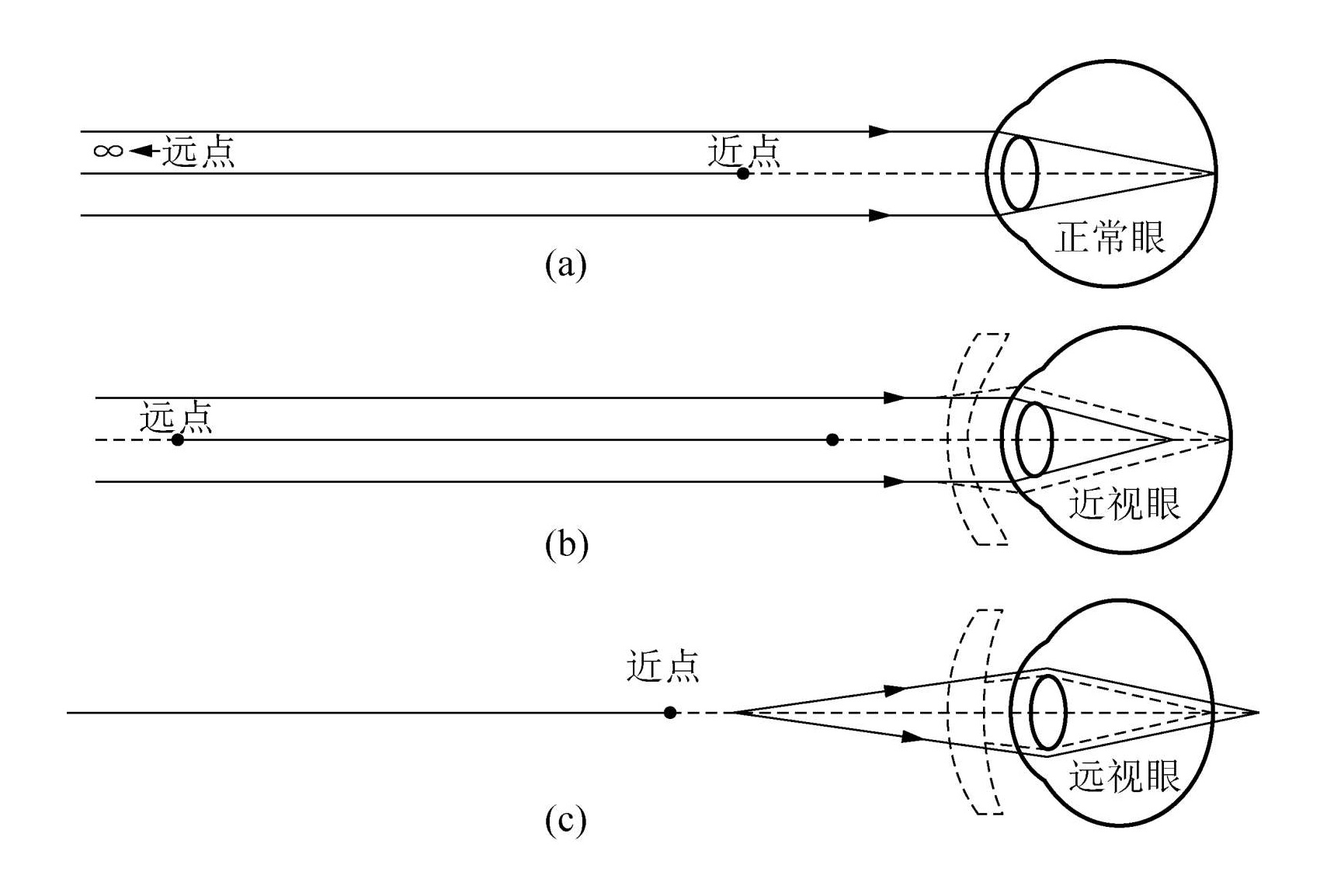
眼睛的第一个概念是远点和近点。眼睛肌肉完全松弛和最紧张时所能清楚看到的点，分别称为它调焦范围的远点和近点。

正常眼睛的远点在无穷远。近视眼睛的眼球过长，当肌肉完全松弛时，无穷远的物体成像在网膜之前，它的远点在有限远的位置。远视眼的眼球过短，无穷远的物体成像在网膜之后，它的远点在眼睛之后，为虚物点。

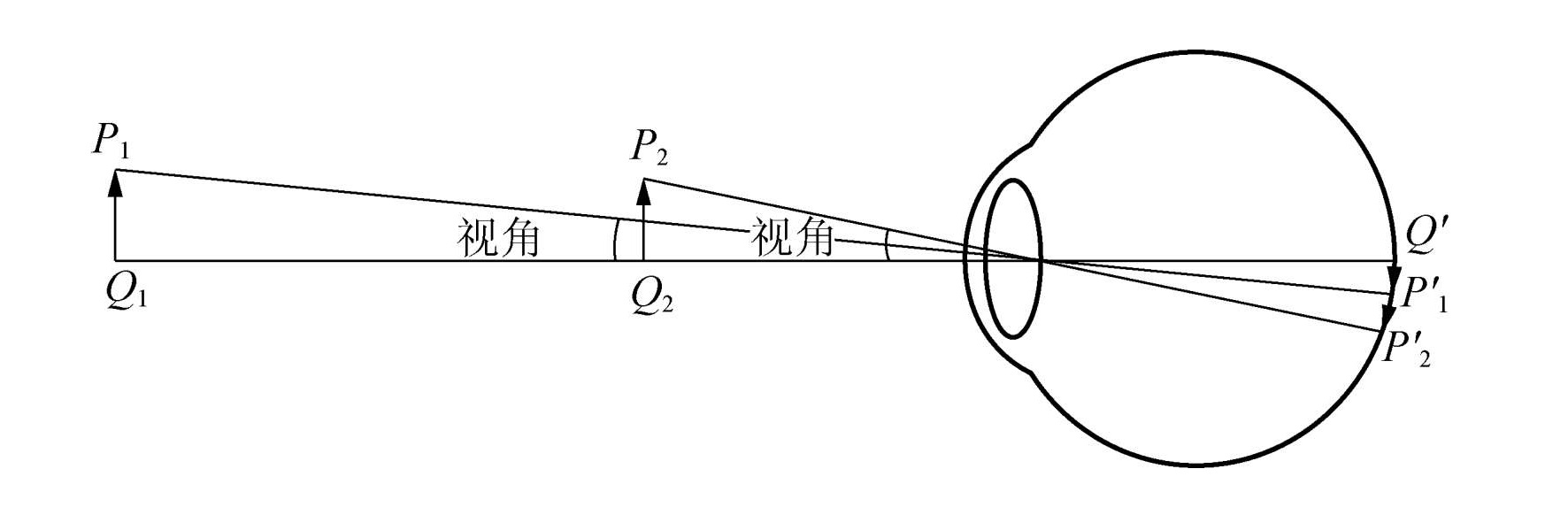
眼睛的第二个概念是明视距离。习惯上规定明视距离就是近点，物体再靠近眼睛则感到疲累，物体在明视距离处时眼睛最舒适。一般人的明视距离 $s_0 = 25 \mathrm{cm}$ ，它是一个比较大的值。由此可以推出高为 $y$ 的物体最大视角为

$$w_0 = \frac{y}{s_0}$$

物体在网膜上成像的大小正比于视角，如图所示。因此物体愈近，它在网膜上的像也就愈大，我们便愈容易分辨它的细节。

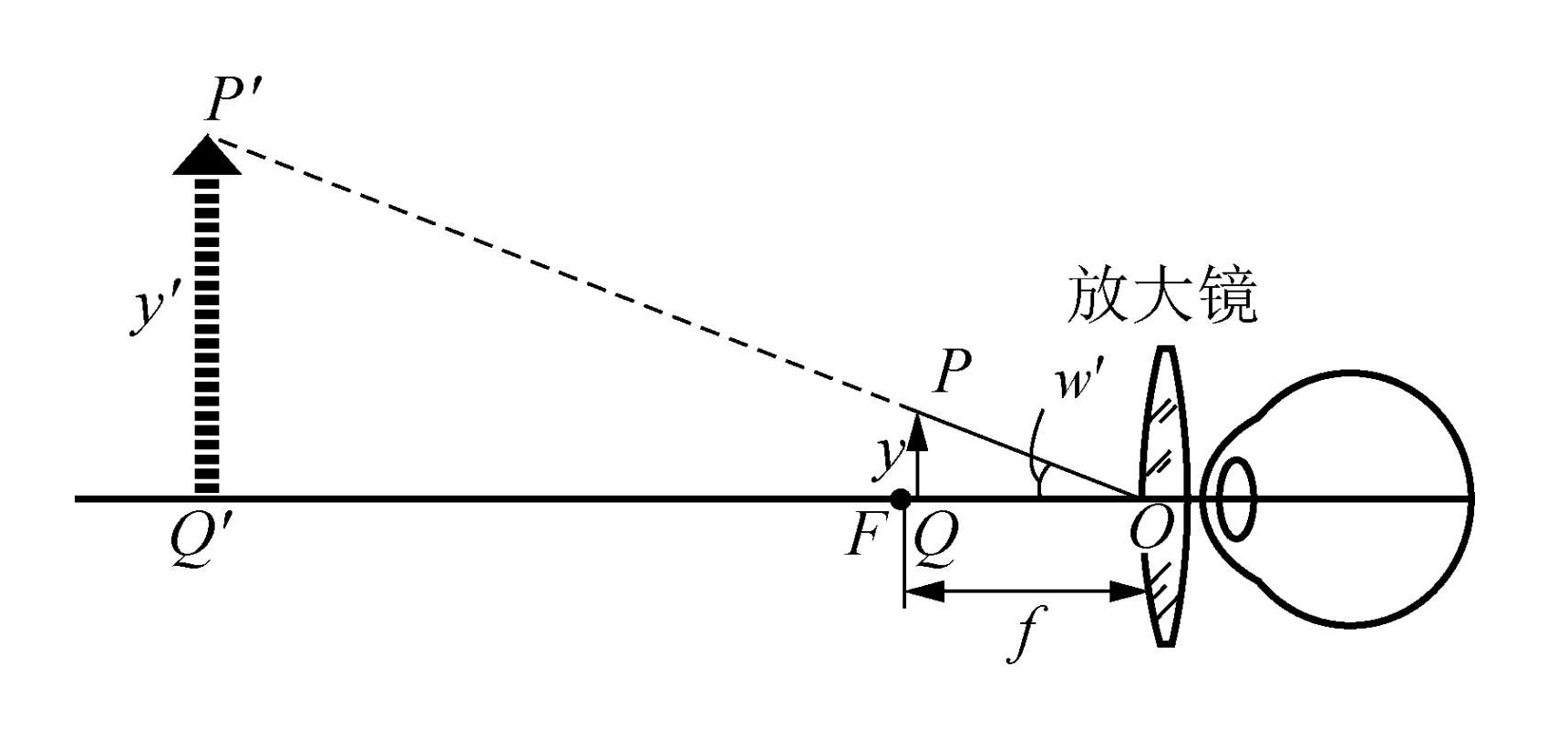
放大镜

放大镜是最基础的光学器件，一般用作复杂光学仪器的最后一步——目镜。

放大镜的目标是，对于在明视距离以内的物体，通过放大镜，将之成像在无穷远点到明视距离之间。

放大镜的焦距 $f$ 的设计应当根据目标来确定，由

$$\frac{1}{s} + \frac{1}{s^\prime} = \frac{1}{f}$$

令 $s < s_0$ ，令 $s^\prime \sim s_0 \sim \infty$ ，并且要求当 $s$ 很大时（例如 $s \to s_0$ ），放大镜失效。从而将 $f$ 设计为 $f \ll s_0$，同时 $s$ 略小于 $f$ 即可。即物体应该放在焦点内侧附近，如图所示。

此时物体的视角为

$$w = \frac{y}{s^\prime} = \frac{y}{s} \approx \frac{y}{f}$$

视角放大率为

$$M = \frac{w}{w_0} = \frac{s_0}{f}$$

视角放大率是最后的像所张的视角 $w$ 与用肉眼观察时物体在明视距离处所张的视角 $w_0$ 之比。

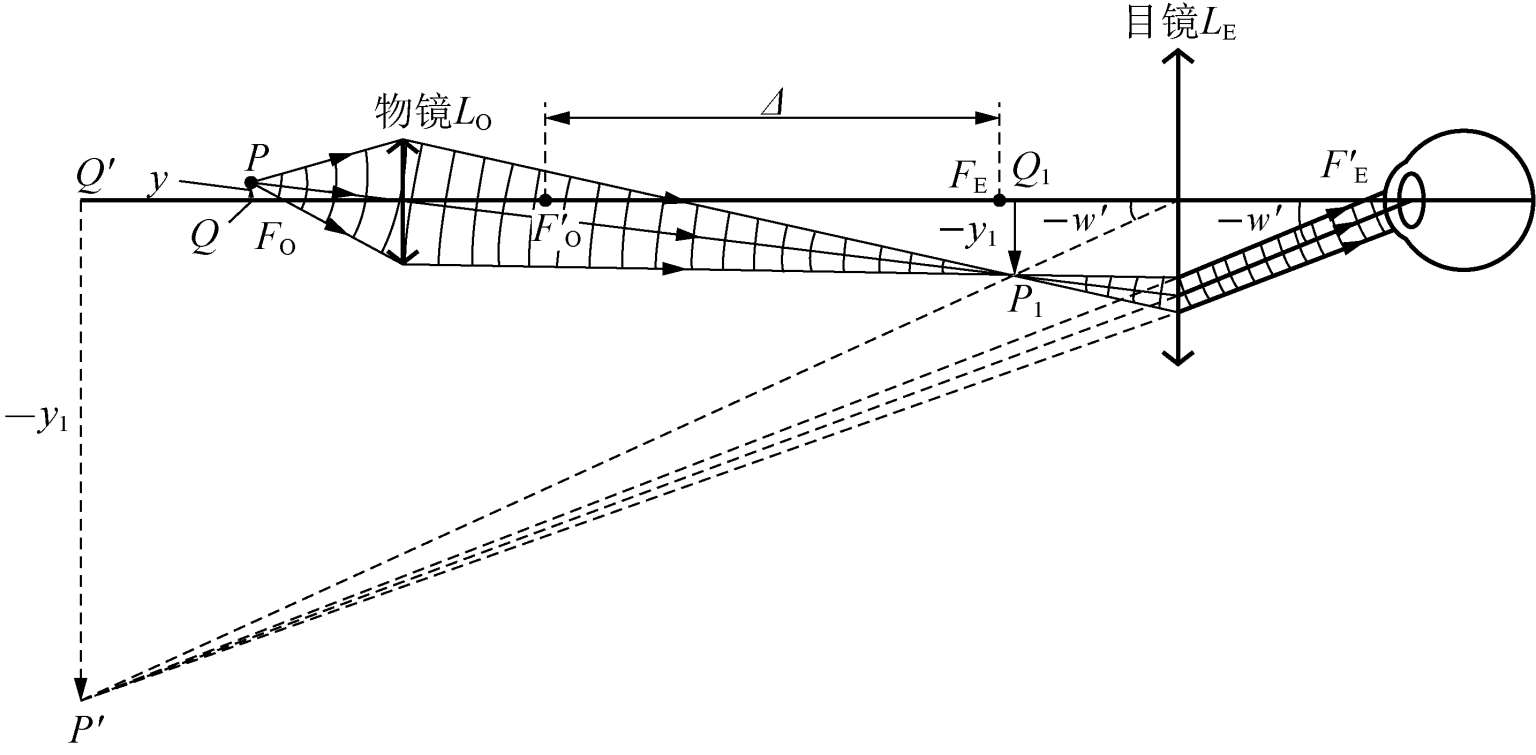
显微镜

显微镜是在放大镜基础上又在前面加了一个凸透镜，即所谓物镜 (Objective lens) ，原来的放大镜称为目镜 (Eye lens) 。

凸透镜的作用是依旧是放大。被观察的物体放在物镜物方焦点 $F_O$ 外侧附近，从而 $x$ 是小量，横向放大率 $V_O = -f/x$ 是大量。

被观察物体先经过物镜一次放大，成像到前述的目镜焦点内侧，再经过目镜第二次放大，从而得到巨大的视角放大率。

$$M = \frac{w}{w_0} = \frac{y_1}{f_E} \Big/\frac{y}{s_0} = \frac{y_1}{y} \frac{s_0}{f_E}= V_O M_E = -\frac{\Delta}{f_O}\frac{s_0}{f_E}$$

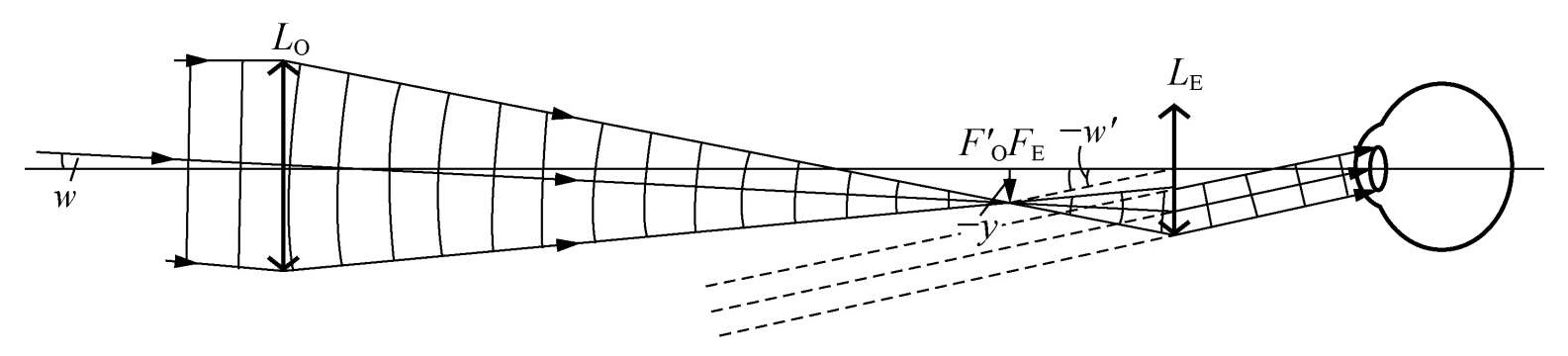
望远镜

望远镜的结构和光路与显微镜有些类似，也是先由物镜成中间像，再通过目镜来观察此中间像。与显微镜不同的是，望远镜所要观察的物体在无穷远处，因此中间像成在物镜的像方焦面上。所以望远镜的物镜焦距较长，而物镜的像方焦点 $F_O^\prime$ 和目镜的第一焦点 $F_E$ 几乎重合。

望远镜的视角放大率定义为最后的像所张的视角 $w$ 与用肉眼观察时物体在无穷远处所张的视角 $w$ 之比。

$$M = \frac{y_1}{f_E} \Big/ \frac{y}{s} = \frac{y_1}{f_E} \Big/ \left( - \frac{y_1}{f_O}\right) = -\frac{f_O}{f_E}$$

光度学基本概念

发光体

点光源沿某一方向的发光强度 $I$ 定义为沿此方向上单位立体角 $\mathrm{d} \Omega$ 内发出的光通量 $\mathrm{d} \Phi$ ，即

$$I = \frac{\mathrm{d} \Phi}{\mathrm{d} \Omega}$$

面光源的发光强度 $I$ 是各面元发光强度的叠加，因此还要再除以一个 $\mathrm{d} S^*$ 定义亮度，即

$$B = \frac{\mathrm{d} I}{\mathrm{d} S^*} = \frac{\mathrm{d} I}{\mathrm{d} S \cos \theta}$$

用规范的语言说就是，面元沿某一方向的光度学亮度 $B$ 定义为在此方向上单位投影面积的发光强度。

被照面

一个被光线照射的表面上的照度定义为照射在单位面积上的光通量。假设面元上 $\mathrm{d} S^\prime$ 的光通量为 $\mathrm{d} \Phi^\prime$ ，则此面元上的照度为

$$E =\frac{\mathrm{d} \Phi^\prime}{\mathrm{d} S^\prime}$$

视见函数

不同波长的光使眼睛产生亮暗感觉的程度不同，因此光的辐射能通量和人眼看见的光通量还有点区别。波长为 $555 \text{nm}$ 的光对人眼来说最敏感，将波长为 $555 \text{nm}$ 的光的辐射通量定义为最大光功当量 $\Phi_{555}$ ，而其他波长的光就得乘一个比例系数 $V(\lambda)$ ，从而混杂着各种波长的光在人眼里的实际光通量为

$$\Phi = \Phi_{555} \int V(\lambda)\, \mathrm{d}\lambda$$