光学笔记（五）光在晶体中的传播

本文讨论光在各向异性介质中的传播。在各向异性介质中我们主要讨论晶体，但也不完全限于晶体。对于光本身，在这里突出的是它的偏振态的改变问题。

基本概念

晶体的分类

单轴晶体：冰洲石，石英，红宝石，冰

双轴晶体：云母，蓝宝石，橄榄石，硫黄

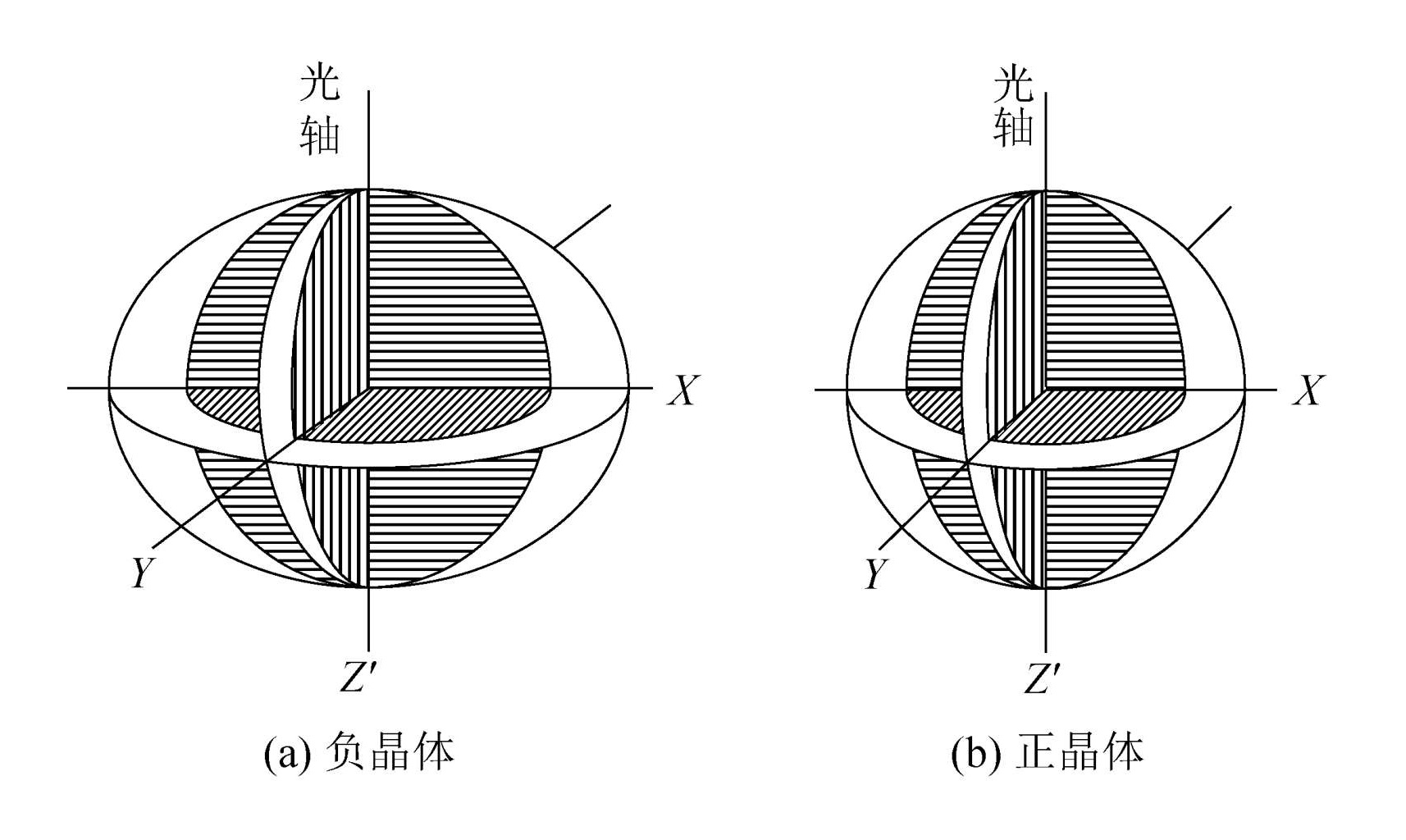
正晶体：$v_o > v_e$，$n_o < n_e$，以石英为代表

负晶体：$v_o < v_e$，$n_o > n_e$，以冰洲石为代表

晶体平面

晶体平面是为了方便描述和确定光的传播方向与振动方向而定义的。

1. 主截面：界面的法线与晶体的光轴组成的平面，称为主截面。
2. 主平面：晶体中某条光线与晶体光轴构成的平面，叫做主平面。
3. 入射面：界面的法线与光线构成的平面，称为入射面。

o光与e光

性质1：$o$ 光沿任意方向传播的速度 $v_o$ 相同，其波面是球面；$e$ 光沿光轴方向的传播速度与 $o$ 光一样，也是 $v_o$，垂直光轴方向的传播速度是另一数值 $v_e$ 。对于任意光线方向，设光线方向与光轴的夹角为 $\theta$ ，则

$$\frac{1}{n^2(\theta)} = \frac{\cos^2 \theta}{n_o^2} + \frac{\sin^2 \theta}{n_e^2}$$

$$v(\theta) = \frac{c}{n(\theta)}$$

性质2：$o$ 光电矢量的振动方向与主平面垂直， $e$ 光电矢量的振动方向在主平面内。

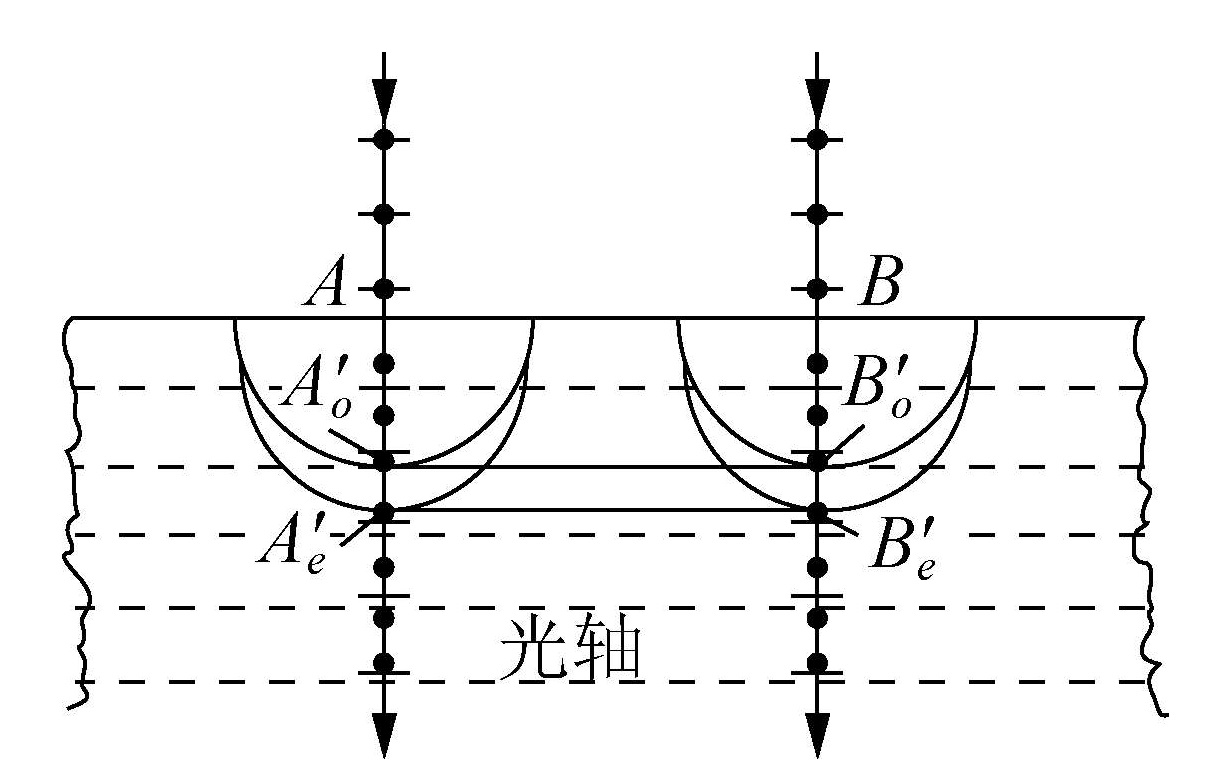
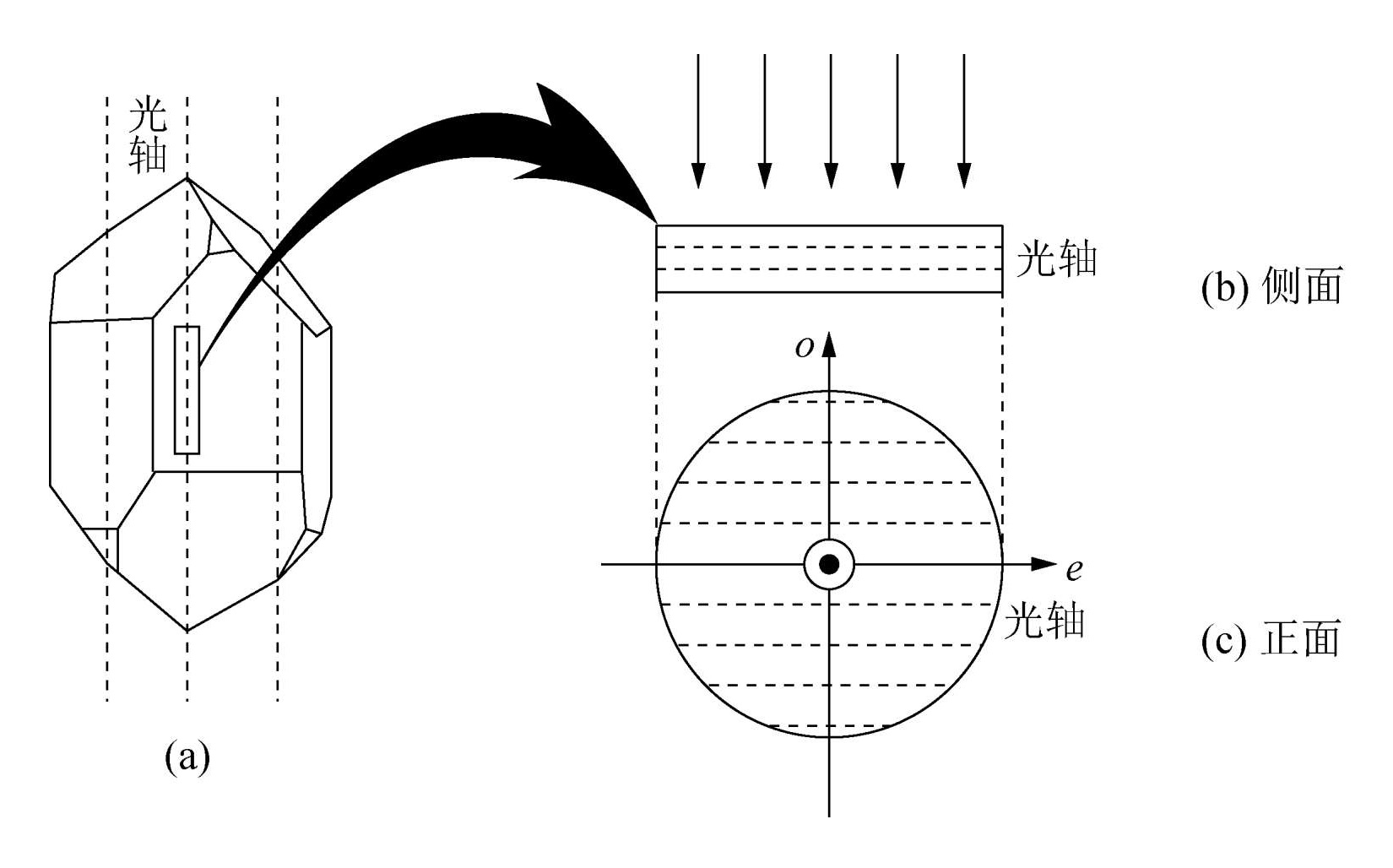
如图所示的负晶体冰洲石中，主平面为纸面。因此 $-$ 标记的为 $e$ 光，$\bullet$ 标记的为 $o$ 光。

性质3：$o$ 光的波面是球面，$e$ 光的波面是回转椭球面。

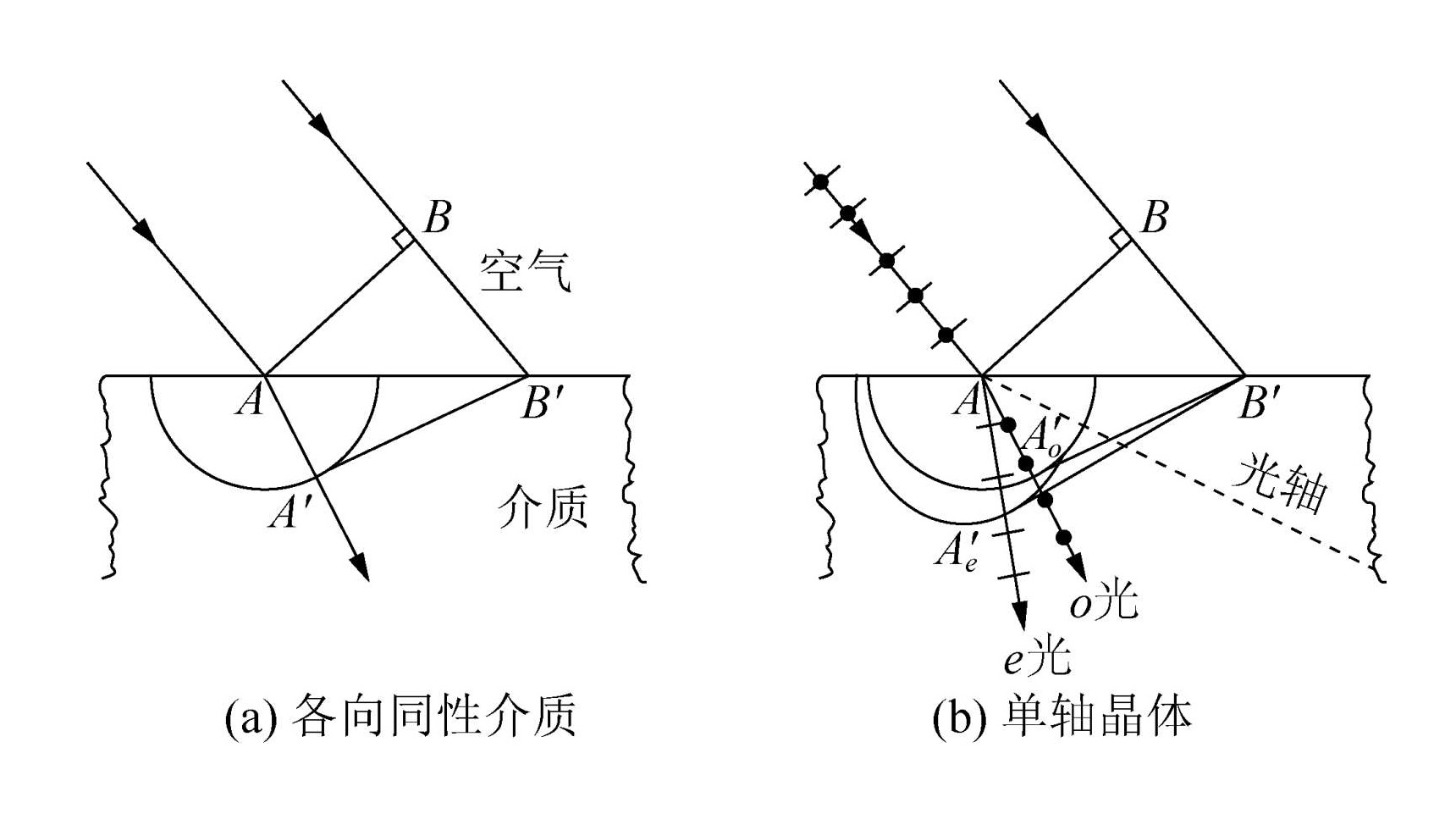
晶体的惠更斯作图法

1. 画出平行的入射光束，令两边缘光线与界面的交点分别为 $A,B$ 。
2. 由先到界面的 $A$ 点作另一边缘入射线的垂线 $AB$ ，它便是入射线的波面。求出 $B$ 到 $B^\prime$ 的时间 $t=\overline{B B^\prime} /c$ 。
3. 以 $A$ 为中心，$v_ot$ 为半径，在折射介质内作半圆，这就是另一边缘入射线到达 $B^\prime$ 点时由 $A$ 点发出的 $o$ 光次波面。再作一个与它在光轴方向上相切的半椭球面，其另外的半主轴长为 $v_e t$，这就是 $e$ 光的次波面。
4. 通过 $B^\prime$ 点作上述半圆的切线，这就是折射线的波面。
5. 从 $A$ 连接到切点 $A^\prime$ 的方向便是折射线的方向。

晶体光学器件

晶体偏振器

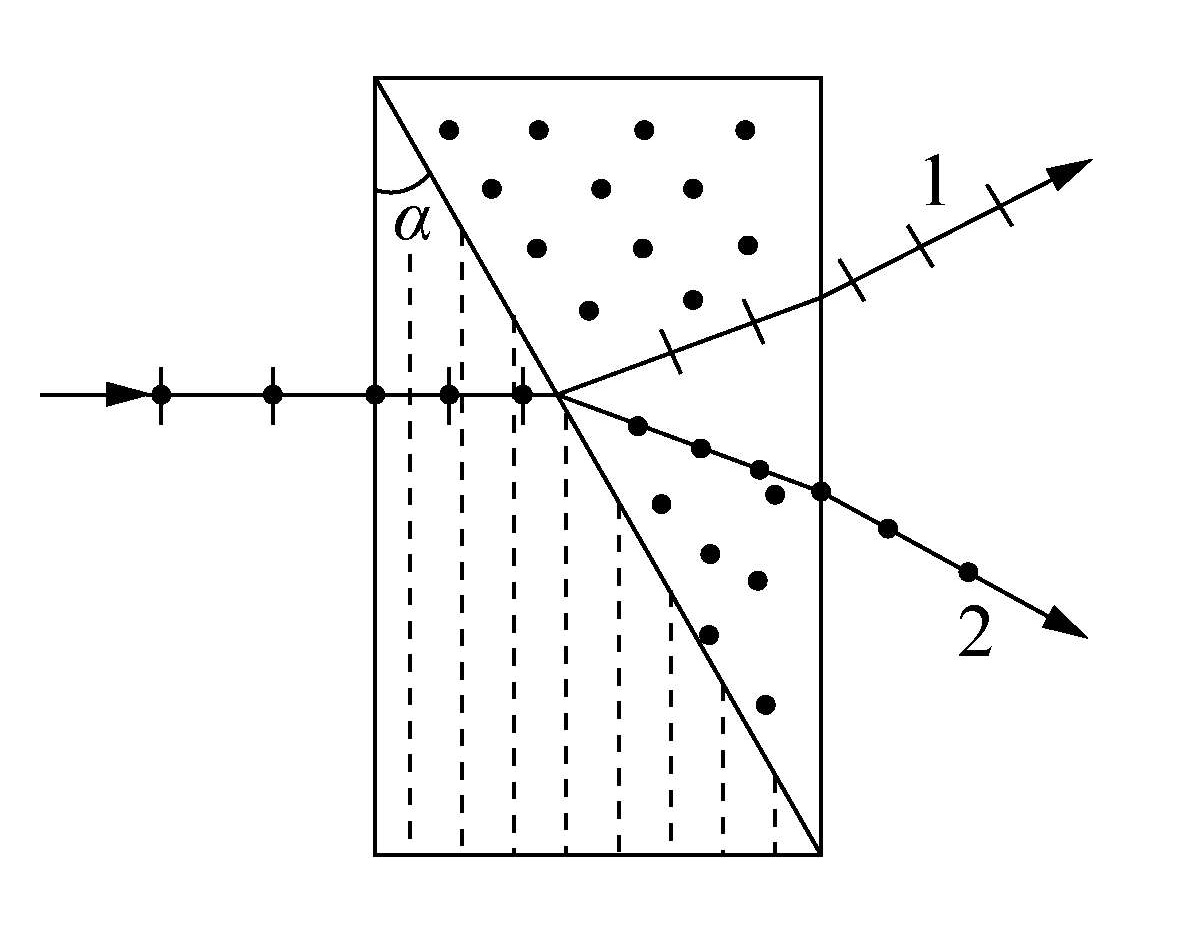
Wollaston棱镜是由两块冰洲石的直角三棱镜粘合而成的。第一块冰洲石棱镜的光轴与入射界面平行，第二块冰洲石棱镜的光轴与入射面垂直。在两块冰洲石的分界面上，由于光轴的转变，原来的 $o$ 光变成了 $e$ 光，原来的 $e$ 光变成了 $o$ 光。

波晶片

波晶片是从单轴晶体中切割下来的平行平面板，波晶片的表面与光轴平行。

当一束平行光正入射时，分解成的 $o$ 光和 $e$ 光传播方向虽然不改变，但它们在波晶片内的速度 $v_o,v_e$ 不同 ，或者说波晶片对于它们的折射率 $n_o = c/v_o, n_e = c/v_e$ 不同。设波晶片的厚度为 $d$，则 $o$ 光和 $e$ 光通过波晶片时的光程也不同。相位差为

$$\Delta = \varphi_o-\varphi_e=\frac{2\pi}{\lambda}(n_o-n_e)d$$

适当地选择 $d$ ，可以制作不同的相位延迟片

• $\lambda/4$ 片：厚度满足 $(n_o-n_e)d=\pm \lambda/4$ ，$\Delta = \pm \pi/2$
• $\lambda/2$ 片：厚度满足 $(n_o-n_e)d=\pm \lambda/2$ ，$\Delta = \pm \pi$
• 全波片：厚度满足 $(n_o-n_e)d=\pm \lambda$ ，$\Delta = \pm 2\pi$

偏振光的干涉

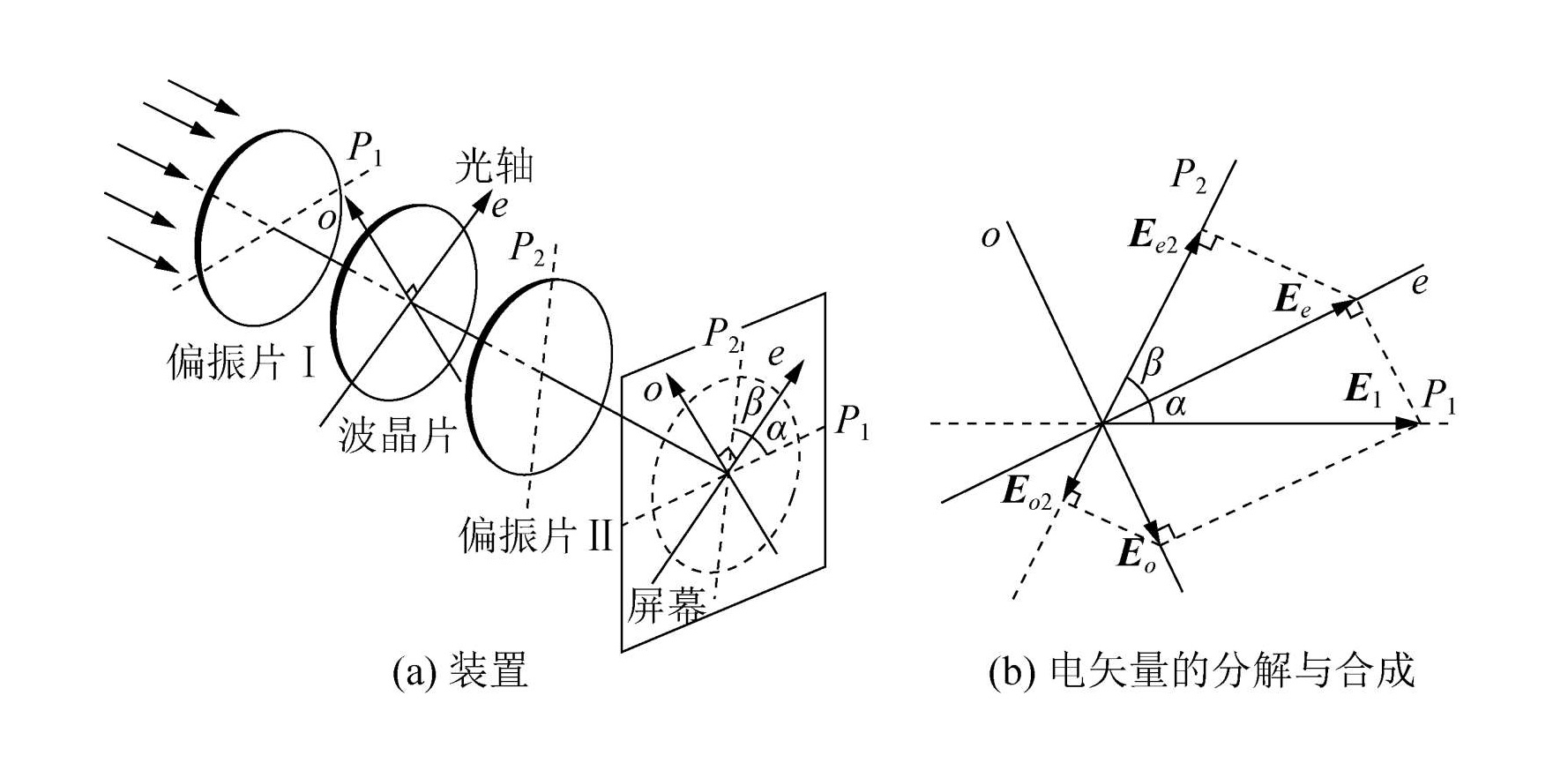
如图所示在两偏振片Ⅰ，Ⅱ之间插入一块厚度为 $d$ 的波晶片，三元件的平面彼此平行，光线正入射到这一系统中。

设 $e$ 轴与 $P_1$ 轴的夹角为 $\alpha$ ， 与 $P_2$ 轴的夹角为 $\beta$ ，两个振动之间的相位差为 $\delta$ ，则可得

$$I_{2} =A_{1}^{2}\left(\cos ^{2} \alpha \cos ^{2} \beta+\sin ^{2} \alpha \sin ^{2} \beta+2 \cos \alpha \cos \beta \sin \alpha \sin \beta \cos \delta\right)$$

其中两个振动之间的相位差 $\delta$ 由三部分组成：

1. 入射光原有的 $e$ 光与 $o$ 光的相位差 $\delta_\text{i}$ ；
2. 坐标轴投影引起的相位差 $\delta_\text{proj}$ ：若 $e$ 轴和 $o$ 轴的正向对 $P_1$ 轴和 $P_2$ 轴的两个投影分量方向一致，则 $\delta_\text{proj} = 0$ ，若两个投影分量方向相反，则 $\delta_\text{proj} = \pi$ ；
3. 由波晶片引起的相位差 $\Delta$ ： $o$ 光和 $e$ 光的附加相位差为 $\Delta =\dfrac{2\pi}{\lambda}(n_e-n_o)d$ 。