LaTeX技巧
fengxiaot Lv4
  2022-01-29 23:16:22 2022-01-29 23:16  

本文收录一些作为数学/物理工作者在使用 LaTeX\LaTeX 过程中可能遇到的困难，调用的宏包，以及一些规范与技巧，属于长期更新向。

基础输入

三线表

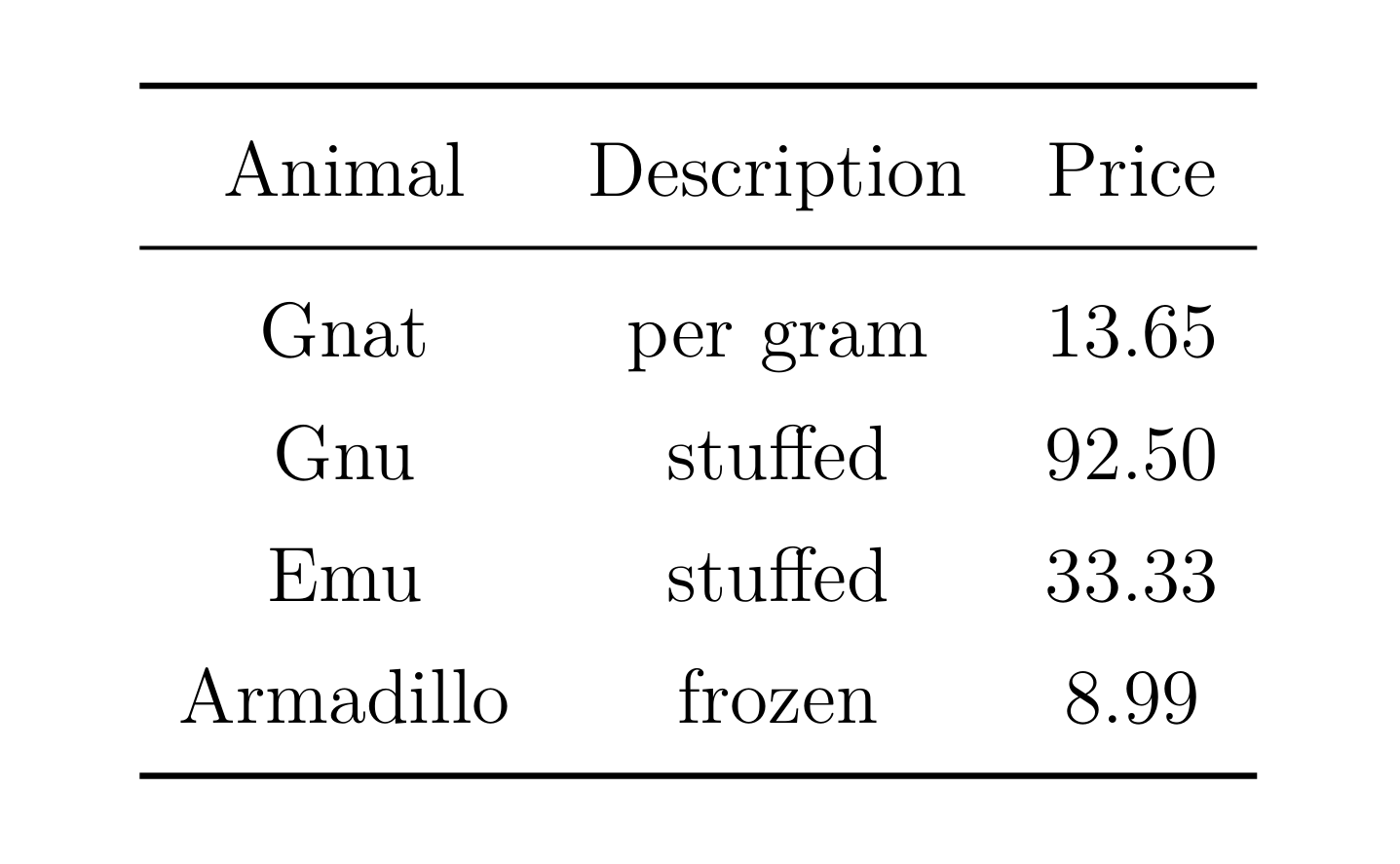
一般论文或书籍中，最常使用的表格样式便是三线表，需要使用 booktabs 宏包引入，即

1
\usepackage{booktabs}

引入此宏包后，三线表的三条线分别可以使用指令 \toprule ，\midrule 和 \bottomrule 实现，例如下面的代码

1
2
3
4
5
6
7
8
9
10
\begin{tabular}{ccc} 
    \toprule
    Animal & Description & Price \\ 
    \midrule
    Gnat & per gram & 13.65 \\
    Gnu & stuffed & 92.50 \\
    Emu & stuffed & 33.33 \\
    Armadillo & frozen & 8.99 \\ 
    \bottomrule
\end{tabular}

将会给出

行距

LaTeX中默认的表格行距一般过紧，需要引入 array 宏包进行调整，例如

1
2
\usepackage{array}
\renewcommand{\arraystretch}{1.3}

个人感觉1.3是比较合适的行距，可以根据视觉效果自行进行调整。

基础数学

微分算符

微分算符 d\mathrm{d} 是数学正体，因此排版时应当格外注意。在国际标准 ISO 80000-2:2009 中，微分算子被描述为

  • 直立的拉丁字母 d\mathrm{d}
  • 一个右边没有间距的操作符

因此常见的做法是使用 \mathrm{d} 输入，这是非常正确的。然而，微分算子有时需要左边有一个小间距，最常见的情况是积分

∫f(x) dx\int f(x) \, \mathrm{d}x

在规范排版中，f(x)f(x) 应当与 dx\mathrm{d} x 之间有 1/6 em1/6 \ \mathrm{em} 的小空格，即使用一个 \, 输出。但是对于处在其他位置的微分算符来说，前面却不需要有小空格。合理的定义是[1]

1
\newcommand*{\dif}{\mathop{}\!\mathrm{d}}

尽管如此，作者还是推荐统一使用 derivative 宏包里的各项命令，使用 \dd 系列来输出微分算符。

1
\odif x  \dd[3]{x}  \dv{x}  \dv{f}{x}  \dv[n]{f}{x}

将分别给出

dxd3xddxdfdxdnfdxn\mathrm{d}x \quad \mathrm{d}^3 x \quad \frac{\mathrm{d}}{\mathrm{d} x} \quad \frac{\mathrm{d} f}{\mathrm{d}x} \quad \frac{\mathrm{d}^n f}{\mathrm{d} x^n}

毕竟，造轮子不如用轮子，而且这个轮子还是经历过万千物理工作者检验的。

曲面积分

LaTeX 并不原生支持二重曲面积分 \oiint

\oiint\oiint

因此最美观的情况可以使用

1
\int\kern{-8pt}\int \mkern{-24mu} \bigcirc

来输出

∫∫◯\int\kern{-8pt}\int \mkern{-24mu} \bigcirc

当然还有一个替代的选择是引入 unicode-math 宏包使得 \oiint 指令可以使用

二重极限

二重极限和二重求和可以使用 \substack 指令给出

1
\lim_{\substack{x \to x_0 \\ y \to y_0}}        \sum_{\substack{0<i<m\\0<j<n}}

lim⁡x→x0y→y0∑0<i<m0<j<n\lim_{\scriptstyle {x \to x_0} \atop \scriptstyle{y \to y_0}} \sum_{\scriptstyle {0<i<m} \atop \scriptstyle{0<j<n}}

关系标注

带标注关系运算符可以通过 \stackrel 指令给出，例如

1
\stackrel{W}{\sim} \stackrel{\mathrm{MnO}}{\longrightarrow}

∼W⟶MnO\stackrel{W}{\sim} \qquad \stackrel{\mathrm{MnO}}{\longrightarrow}

物理宏包

量子力学

量子力学中需要输入左矢和右矢，braket 宏包给出了自然的命令

1
\bra{\psi}    \ket{\psi}    \braket{\varphi | A | \psi}

分别给出左矢，右矢和内积

⟨ψ∣∣ψ⟩⟨φ∣A∣ψ⟩\langle \psi | \quad | \psi\rangle \quad \langle \varphi | A|\psi\rangle

若希望 bra-ket 的大小随着算符的大小而调整，则可以使用首字母大写的 \Bra{} ，\Ket{} ，与 \Braket{} 。例如，下列代码给出

1
\braket{\varphi | \frac{\partial}{\partial t} | \psi}    \Braket{\varphi | A | \psi}

相对论

相对论中需要输入张量，并且要求指标有先后顺序，需要引入 tensor 宏包。如果要输入有先后顺序的指标，需要将指标放入 \indices{} 指令的花括号中。例如洛伦兹张量的输入为

1
x^{\prime\mu} = \Lambda\indices{^\mu_\nu} x^{\nu}

上述代码将会给出

x′μ=Λμν xνx^{\prime\mu} = \Lambda{^\mu}{_\nu} \, x^{\nu}

  1. 在 LaTeX 中使用微分算子的正确姿势 https://liam.page/2017/05/01/the-correct-way-to-use-differential-operator/ ↩︎