光学笔记（三）干涉装置

本文梳理一下常见的干涉装置，插图主要来自钟锡华老师和赵凯华老师合编的《光学》。

等厚干涉

干涉公式

等厚干涉并不等厚，而是一束平行光垂直入射或斜入射到厚度变化的介质内，介质上下表面处的反射光产生的干涉现象。

设 $i$ 为折射角，则两束光的几何路程差为

$$\Delta L = ABP-CP=2nh \cos i$$

当 $n_1 < n > n_2$ 或 $n_1 > n < n_2$ 时，有半波损，最终光程差还要加上 $\lambda/2$ ；

当 $n_1 < n < n_2$ 或时 $n_1 > n > n_2$ 没有半波损，$\Delta L$ 就是最后的光程差。

正入射

实际应用中最多的是正入射，此时 $i=0$ ，几何路程差为

$$\Delta L =2nh$$

因此相邻等厚条纹对应的厚度差为

$$\Delta h = \frac{\lambda}{2n}$$

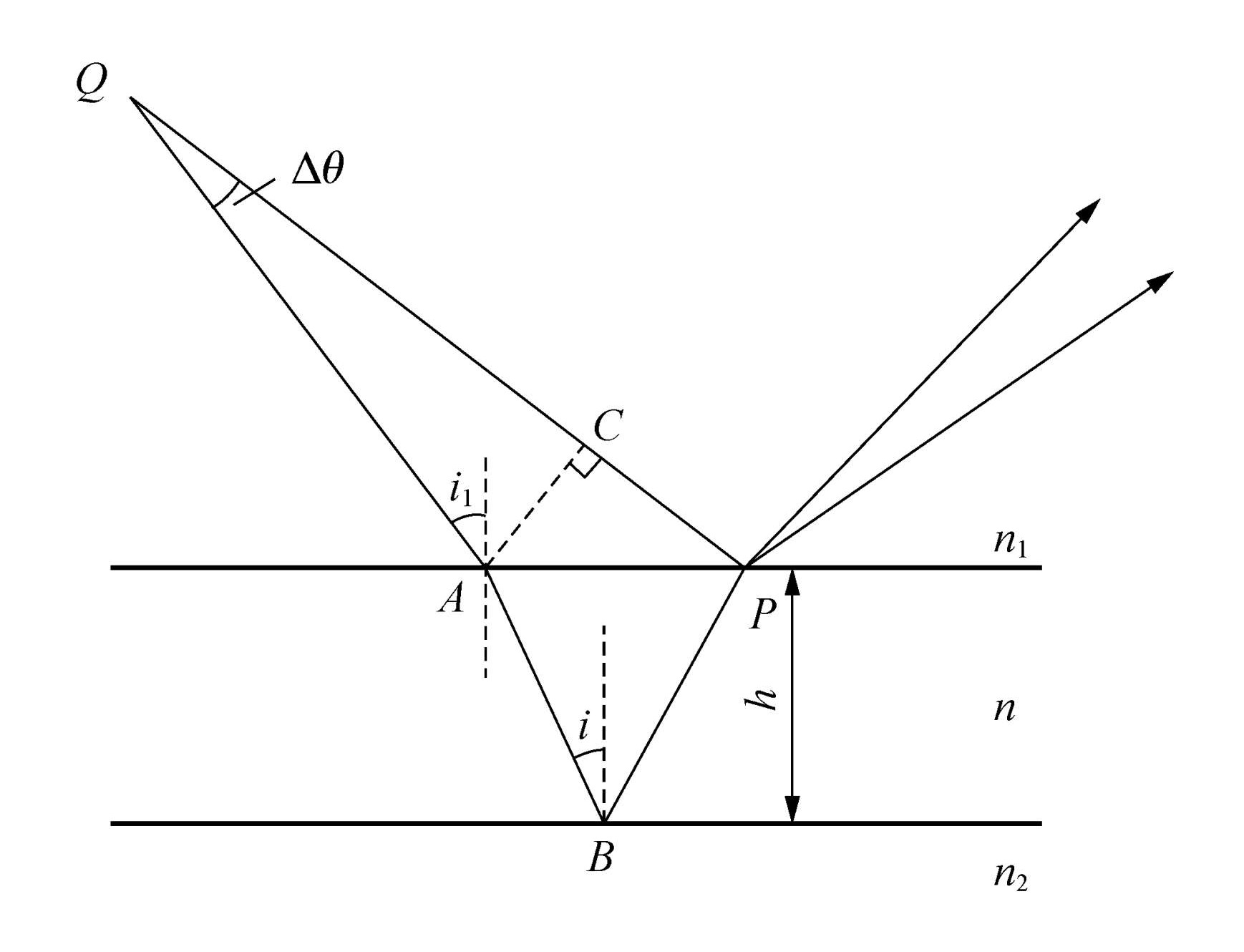
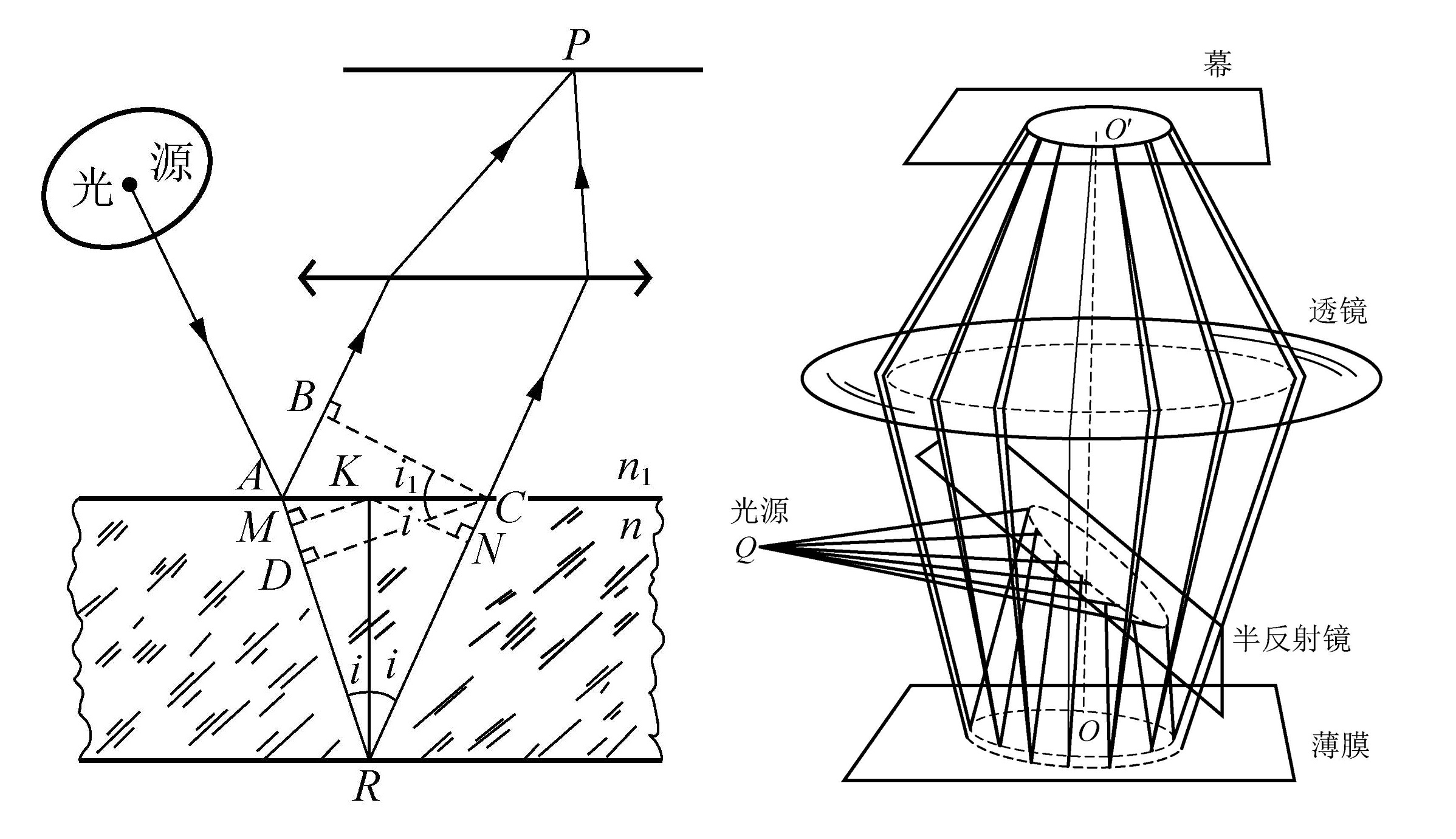
等倾干涉

等倾干涉并不等倾，而是由点光源发出的一束束不同倾角的光，每束具有特定倾角的光在薄膜上产生等倾角的2束反射光，经过凸透镜汇聚在屏幕上同一处产生的干涉。

凸透镜汇聚的原理是斜入射平行光作图法，出射光线必过焦平面上的副焦点，因此等倾角的平行光发生相互干涉。

等倾干涉公式仍然是

$$\Delta L = ARC-AB=2nh \cos i$$

其中 $i$ 为折射角，并且此处未考虑半波损失，实际应用中应当依照具体物理情景取舍 $\lambda/2$ 。

等倾干涉条纹具有以下特点：

1. 等倾干涉条纹为一系列同心圆环，内疏外密，内圆纹的级次比外圆纹的级次高。
2. 膜厚变化时，条纹发生移动。当薄膜厚度增大时，圆纹从中心冒出。
3. 使用面光源条纹更清楚明亮。
4. 透射光图样与反射光图样互补。

关于特点1需要进行一些说明。条纹级次的定义为，第 $k$ 级亮纹满足

$$2nh \cos i_k =k\lambda$$

內圆纹对应的 $i_k$ 小，从而 $\cos i_k$ 大，导致 $k\lambda$ 大，从而级次高，反之外圆纹级次低。而关于条纹的疏密，当倾角不大时可近似认为相邻条纹半径之差 $r_{k+1} - r_k$ 正比于倾角之差 $i_{k+1} - i_k$ ，这一点从上面的3D图可以观察出来。那么简单推导可知

$$\begin{aligned} \cos i_{k+1}-\cos i_{k} & \approx \left(i_{k+1}-i_{k}\right) \frac{\mathrm{d} \cos i}{\mathrm{~d} i}\bigg| _{i=i_{k}} \\ &=-\sin i_{k}\left(i_{k+1}-i_{k}\right) \end{aligned}$$

从而

$$\Delta r=r_{k+1}-r_{k} \propto i_{k+1}-i_{k}=\frac{-\lambda}{2 n h \sin i_{k}}$$

式中负号表明上述 $r_{k+1} < r_k$ 的事实。由分母上的 $\sin i_k$ 便知内疏外密。

关于特点3也要进行说明，只有光程差为 $k\lambda$ 的条纹才叫第 $k$ 级亮纹！即使膜厚变大，条纹级数与光程差的一一对应关系仍然不变。因此当 $h$ 增大时，若使 $k\lambda$ 不变，$\cos i_k$ 应当减小，即 $i_k$ 增大，对应倾角变大，因此第 $k$ 级条纹向外移动，即所谓圆纹从中心冒出。

牛顿环

牛顿环是一种分振幅干涉装置。设第 $k$ 级暗纹的半径为 $r_k$ ，透镜曲率半径为 $R$ ，则

$$r_k^2 = k R\lambda$$

增大透镜与平板玻璃间的距离，干涉条纹向中心收缩，膜厚每增大 $\lambda/4$ ，条纹就向中心收缩一条。

/* 再次强调：只要条纹还是那一级的条纹，那么它的光程差还是那个光程差。即使某条纹移动了，它还是那一级的条纹。条纹级数的唯一决定因素是光程差的大小。 */

Explanation

牛顿环是等厚干涉，平凸透镜上移时空气层厚度增加，那么某条纹它要保证自己还是那一级的条纹，它就要保持和原来一样的光程差，所以此时它得往中间空气层厚度小的地方移动，以保持和原来的光程差相等。即向中心收缩。

若接触良好，则中央为暗纹，中间的空气层不可忽略，再接触良好也有半波损失。

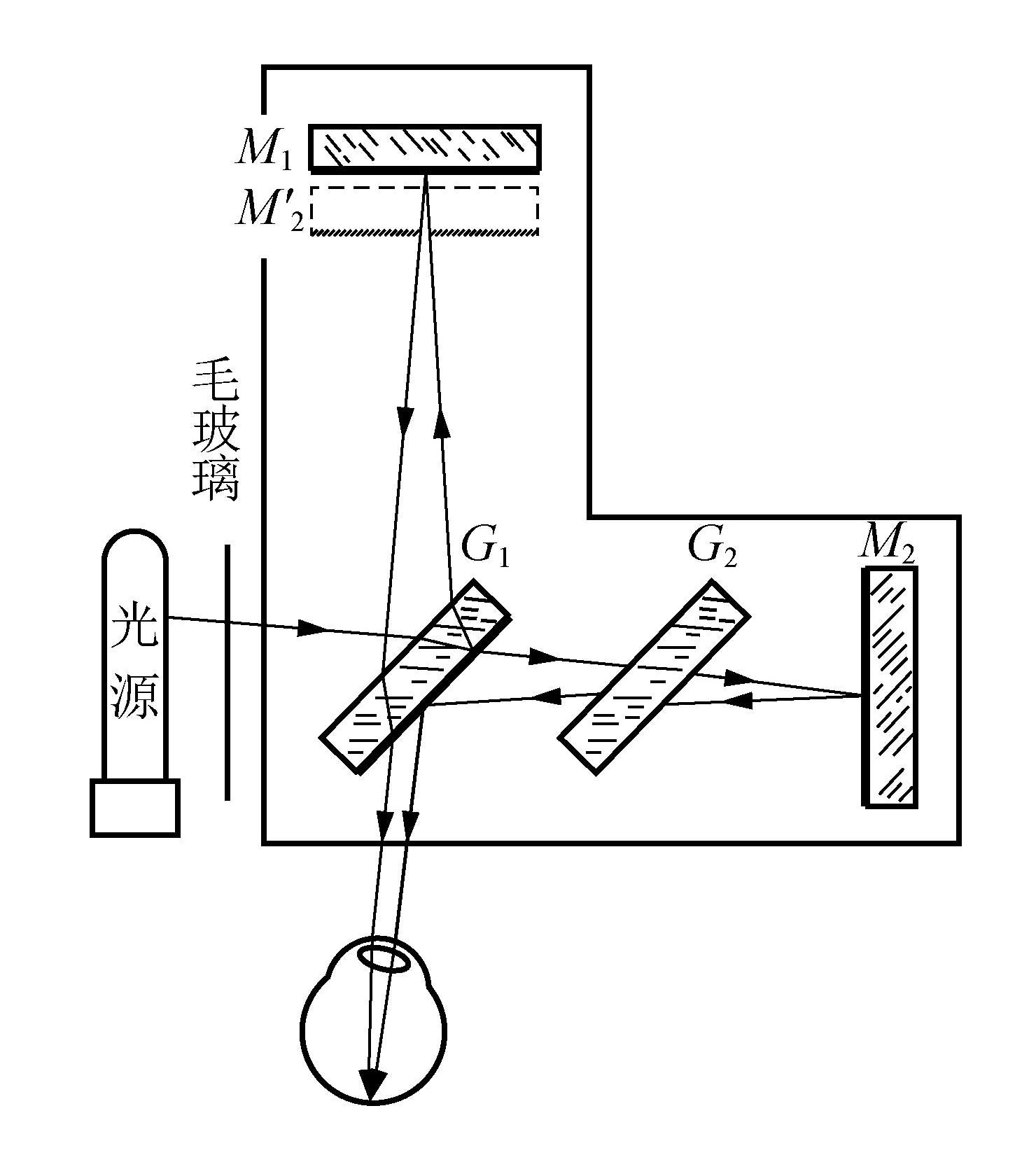
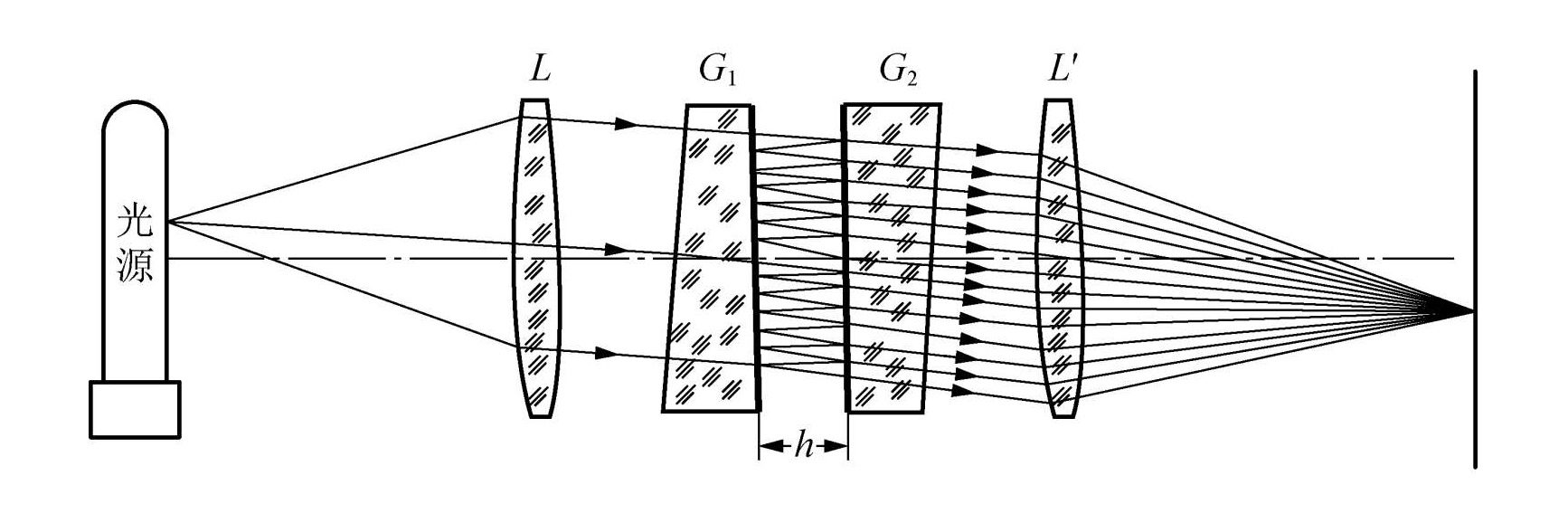
迈克尔逊干涉仪

基本原理

迈克尔逊干涉仪是一种分振幅干涉装置，其光路图如图所示。

当 $M_1$ 和 $M_2^\prime$ 平行时，体现为等倾干涉；当 $M_1$ 和 $M_2^\prime$ 有倾角时，体现为等厚干涉。

若 $M_1$ 和 $M_2^\prime$ 虽有倾角但距离太远，时间相干性就被破坏，等厚干涉失效。

迈克尔逊干涉仪没有半波损失，因此第 $k$ 级亮纹就是

$$2nh \cos i_k =k\lambda$$

分析方法与等厚干涉/等倾干涉一致。

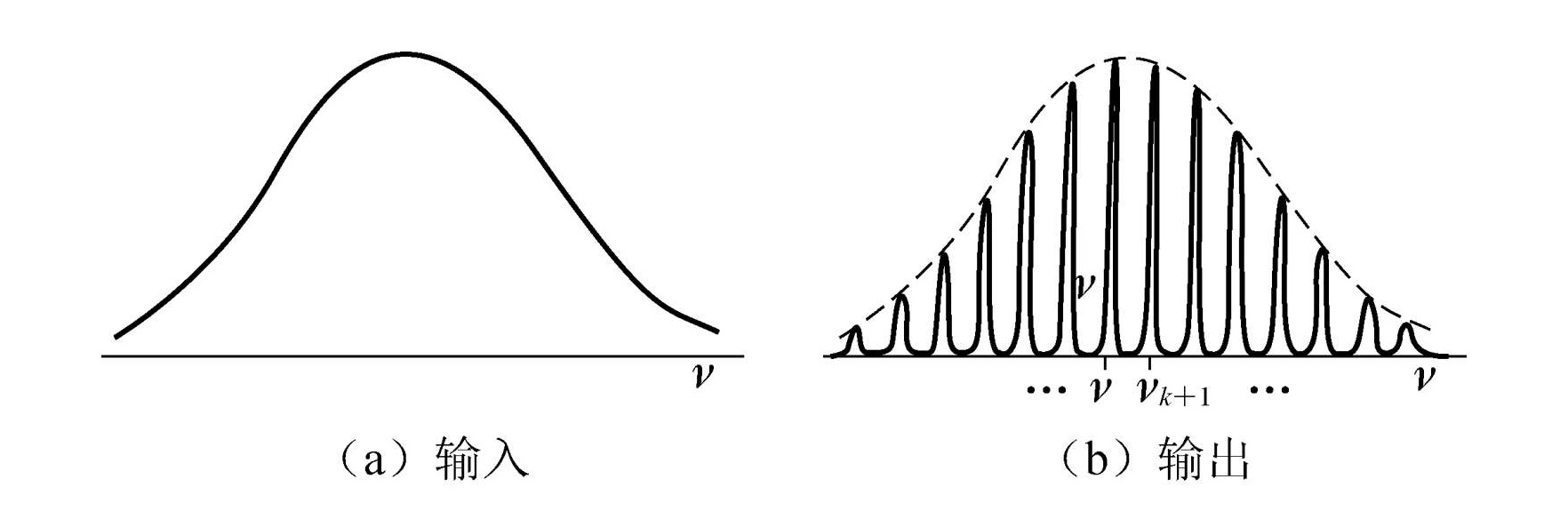
光源的非单色性对干涉条纹的影响

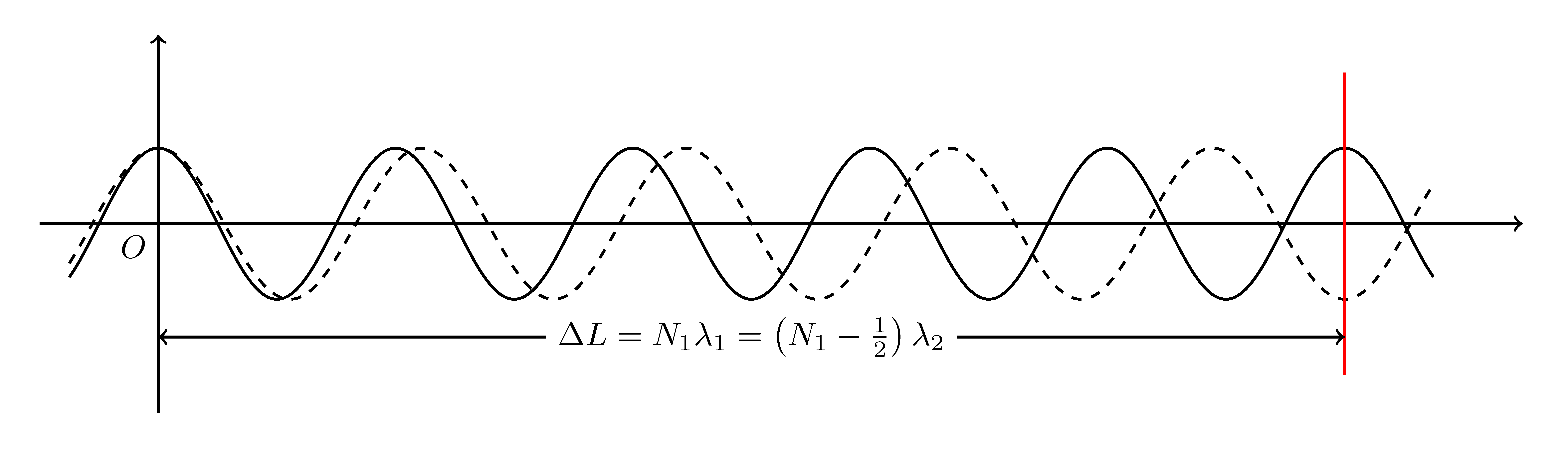
双线结构使条纹衬比度随 $\Delta L$ 作周期性变化，以钠光灯照射为例。设开始时两臂等光程，这时衬比度为1，条纹清晰。现移动一臂中的镜面以改变光程差 $\Delta L$ 。由于两谱线波长 $\lambda_2>\lambda_1$ ，光强的峰与谷逐渐错开，条纹的衬比度下降。图中虚线波长较长，对应 $\lambda_2$ ，实线波长较短，对应 $\lambda_1$ 。

直到错过半根条纹，一个的峰与另一个的谷恰好重叠时，衬比度降到0，条纹不见了，视场完全模糊。这时两套条纹移过视场中心的根数之 $N_1,N_2$ 间有如下关系：

$$\Delta L =N_1 \lambda_1 = \left(N_1 - \frac{1}{2} \right) \lambda_2$$

换言之 $N_2 = N_1 - \frac{1}{2}$ 。由此解得

$$N_{1}=\frac{\lambda_{2}}{2\left(\lambda_{2}-\lambda_{1}\right)}=\frac{\lambda}{2 \Delta \lambda}$$

继续移动镜面，当视场中心再移过这么多根条纹时，两套条纹的峰与峰、谷与谷重新重合，衬比度完全恢复。如此下去，周而复始。由此可见，衬比度变化的空间周期是

$$\Delta L_M=2N_1 \lambda_1 = \frac{\lambda^2}{\Delta \lambda}$$

另一方面，由于光源非单色性的影响，随着光程差 $\Delta L$ 加大，干涉条纹的衬比度下降，这便限制了干涉测长的量程

$$l_M \le \frac{1}{2} \Delta L_M = \frac{\lambda^2}{2\Delta \lambda}$$

时间相干性

在光学笔记（二）中提过，光源发光过程在时间上是断续的，体现为发射许多断续的波列，从而我们要求分振幅之后的两列波在探测仪器处光程差不能太大。所谓的「不能太大」如何衡量？

我们知道，发光持续时间 $\tau_0$ 和频谱宽度 $\Delta \nu$ 受到 Fourier 变换关系的制约

$$\tau_0 \Delta \nu \approx 1$$

因此光程差 $\Delta L$ 与发光持续时间 $\tau_0$ 的制约，就是 $\Delta L$ 与频谱宽度 $\Delta \nu$ 的制约。由 $\Delta \nu = c \Delta \lambda / \lambda^2$ ，可以进一步转化成光程差 $\Delta L$ 与谱线宽度 $\Delta \lambda$ 的制约，这正是我们在上一小节讨论的内容！由此得到时间相干性的反比公式

$$L_0 \approx \frac{\lambda^2}{\Delta \lambda}$$

其中 $L_0$ 为相干长度，既是能发生干涉的最短波列长度，也是等相位波经过干涉系统错开相位之后，在观察处能够容许的最大光程差。

上述两个公式称为时间相干性的反比公式。

FP干涉仪

基本原理

FP干涉仪实质上是加强版的等倾干涉装置，如图所示。

因此最基本的公式依旧是

$$\Delta L = 2nh \cos i = k \lambda$$

此外，我们不加证明地给出FP干涉仪的半值宽度表达式

$$\varepsilon=\frac{2(1-R)}{\sqrt{R}}$$

其中 $R$ 是光强反射率且 $R = |r|^2$ 。一般说来，辐射强度分布曲线上的两上半最大强度点之间的宽度，称为半值宽度。当强度分布曲线的横坐标为 $\lambda$ 时，称为谱线宽度。当横坐标为 $\nu$ 时，称为频谱宽度。当横坐标为相位 $\delta$ 时，没有特殊的称呼，就泛称为半值宽度。我们这里给出的 $\varepsilon$ 是相位为 $\delta$ 横坐标的 $I-\delta$ 曲线的半值宽度。

下面我们依照情景与变量的不同，分别讨论半值宽度的变化。重新改写FP干涉仪的基本公式，把光程差转化成相位差

$$\delta = \frac{2\pi}{\lambda} \Delta L = \frac{4\pi}{\lambda} nh \cos i$$

在FP干涉仪装置中，折射率 $n$ 和间隔 $h$ 一般是不变的，影响 $\delta$ 值变化的因素有二：倾角 $i$ 和波长 $\lambda$ 。下面分别讨论。

单色光及半角宽度

如果以单色的扩展光入射，则 $\lambda$ 固定，但有各种可能的倾角 $i$ 。因为只有在特定的方向 $i_k$ 上出现干涉极强，我们关心某一级极大附近的半值宽度 $\Delta i_k$ 。此半值宽度可以地近似认为是半角宽度，因为半角宽度严格来说是是中心对称的光学图案由中心对分取其一半的角宽度，使用通过相邻暗纹来确定，而这里的FP干涉图样并不对称。因此就把半光强点的距离，即半值宽度作为半角宽度了。

取 $\delta$ 因 $i$ 变化引起的微分

$$\mathrm{d} \delta = -\frac{4\pi}{\lambda} nh \sin i \mathrm{d}i$$

并令 $\mathrm{d} \delta = \varepsilon$ ，令 $\mathrm{d}i = \Delta i_k$ ，可以得到

$$\Delta i_{k}=\frac{\lambda \varepsilon}{4 \pi n h \sin i_{k}}=\frac{\lambda}{2 \pi n h \sin i_{k}} \frac{1-R}{\sqrt{R}}$$

这就是第 $k$ 级亮纹的半角宽度。

复色光及谱线宽度

如果以非单色平行光入射，则此时 $i$ 固定，它经常是0或接近于0，相位差 $\delta$ 主要是光波 $\lambda$ 的函数。取 $\delta$ 因 $\lambda$ 变化引起的微分

$$\mathrm{d} \delta = - 4\pi nh \cos i \frac{\mathrm{d}\lambda}{\lambda^2}$$

并令 $\mathrm{d} \delta = \varepsilon$ ，令 $\Delta \lambda_{k} = \mathrm{d}\lambda$ ，可以得到

$$\Delta \lambda_{k}=\frac{\lambda^{2} \varepsilon}{4 \pi n h \cos i}=\frac{\lambda^{2}}{2 \pi n h \cos i} \frac{1-R}{\sqrt{R}} = \frac{\lambda}{\pi k} \frac{1-R}{\sqrt{R}}$$

这就是第 $k$ 级亮纹的谱线宽度。用频率表示，则得到频谱宽度

$$\Delta v_{k}=\frac{c \Delta \lambda_{k}}{\lambda^{2}}=\frac{c}{2 \pi n h \cos i} \frac{1-R}{\sqrt{R}}=\frac{c}{\pi k \lambda} \frac{1-R}{\sqrt{R}}$$

纵模及其间隔

此外，当 $i$ 固定时，并不是所有波长的光都能够呈现极大，只有满足

$$2nh \cos i = k \lambda_k$$

的特定波长 $\lambda_k$ 附近才能出现极大。这称为FP干涉仪的选频作用。

用频率 $\nu_k$ 表示，则得到

$$\nu_k = \frac{c}{\lambda_k} =\frac{k c}{2 n h \cos i}$$

每个特定的频率 $\nu_k$ 称为一个纵模。可见相邻的纵模是等间隔的，为

$$\Delta \nu = \nu_{k+1} - \nu_k = \frac{c}{2 n h \cos i}$$

在未指定倾角时，通常默认 $i=0$ ，则

$$\Delta \nu \approx \frac{c}{2 n h}$$

这就是所谓的纵模间隔或频率间隔。注意区分纵模间隔和频谱宽度的符号！

增透膜与增反膜

增透膜：增透膜就是消反射层，要求薄膜上下表面处的反射光相位相差 $\pi$ ，从而两束反射光相消。

增反膜：增反膜就是增反射层，要求薄膜上下表面处的反射光相位相差 $2\pi$ 的整数倍，从而反射光加强。